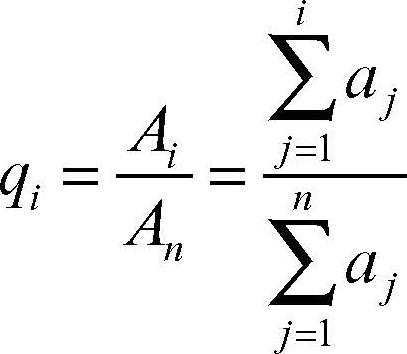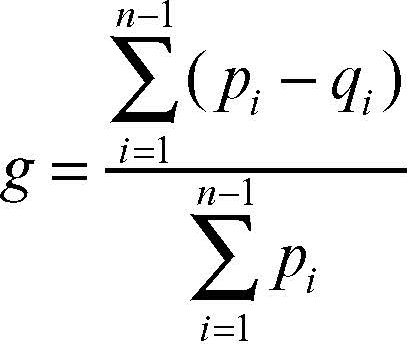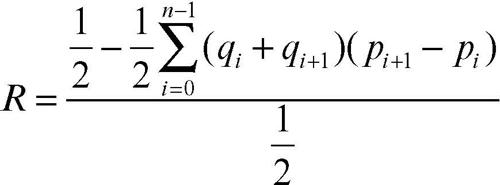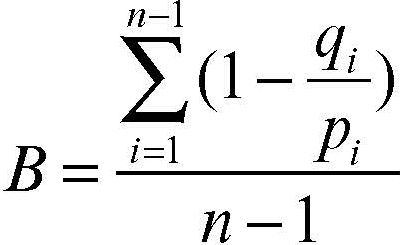concentrazione

concentrazione

concentrazione in statistica, termine che indica il modo in cui si ripartisce tra più unità una data quantità totale (per esempio, l’ammontare globale del reddito di una nazione tra i suoi componenti). Riguarda perciò la distribuzione dell’ammontare complessivo A di un carattere quantitativo che sia trasferibile fra le n unità di un collettivo statistico. La concentrazione è massima quando una sola unità possiede tutto l’ammontare A, minima quando ogni unità possiede la stessa quantità, uguale alla media A/n. La concentrazione cresce con il crescere della porzione di unità statistiche che possiedono il carattere in misura inferiore alla media, cioè assume valore tanto maggiore quanto più unità “povere” ci sono nella popolazione, mentre assume valore minimo in caso di equidistribuzione. Se in un collettivo statistico formato da n unità, si indica con a_i ≥ 0 l’ammontare del carattere posseduto dalla i-ma unità e se le n unità sono ordinate in modo non decrescente rispetto all’ammontare posseduto (per cui: a₁ ≤ a₂ ≤ ... ≤ a_n), allora la somma A_i = a₁ + a₂ + ... + a_i fornisce il totale del carattere posseduto dalle i unità più “povere”.

Il rapporto p_i = i /n indica la frazione delle i unità più “povere” mentre il rapporto

indica la frazione che, sull’ammontare complessivo del carattere, rappresenta l’ammontare che è posseduto dalle i unità più “povere”. Per ogni i = 1, ..., n si ha che q_i ≤ p_i e, in particolare, più i valori di q_i sono vicini a quelli di p_i, minore sarà il livello di concentrazione. Una misura della concentrazione, quindi, deve tenere in considerazione le differenze p_i – q_i, per ogni i = 1, …, n; da qui, poiché p_n = q_n = 1, si ha il rapporto di concentrazione di Gini:

Tale indice assume valori compresi tra 0 e 1 e, in particolare, è uguale a 0 in caso di minima concentrazione mentre è uguale a 1 in caso di concentrazione massima.

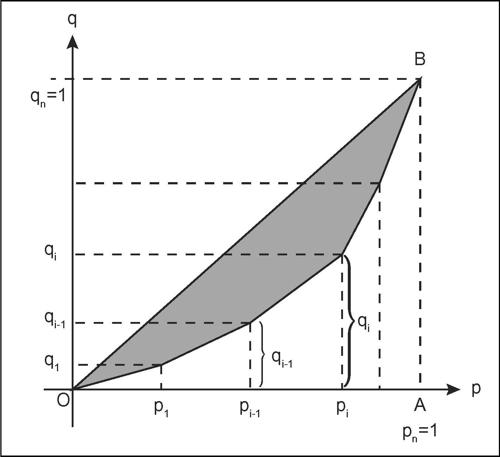
Riportando in un riferimento cartesiano i valori p_i in ascissa e i valori q_i in ordinata, ponendo p₀ = q₀ = 0, e unendo i punti di coordinate (p_i, q_i) per ogni i = 0, ..., n con segmenti, si ottiene la curva di concentrazione (detta anche curva di Lorenz, perché proposta dall’economista statunitense Otto Max Lorenz nel 1905). Nel grafico in figura, il segmento OB (con B di coordinate (1,1)) rappresenta la situazione di perfetta equidistribuzione (corrispondente a una concentrazione minima, uguale a 0) e la curva di Lorenz non è mai al di sopra della retta per OB. Una misura della concentrazione può quindi essere ricavata attraverso il calcolo dell’area di concentrazione, data dall’area della superficie in grigio nella figura. Tale figura poligonale risulta la complementare, rispetto al triangolo OAB, di una somma di trapezi di basi q_i e q_i+1 e la sua area è perciò:

La concentrazione è massima quando tutto l’ammontare è detenuto da una sola unità; in tale caso la superficie descritta è il triangolo OAB. Il rapporto di concentrazione si ottiene perciò dividendo l’area di concentrazione per l’area del triangolo OAB ed è pertanto:

cioè:

Una diversa misura della concentrazione è data dal seguente indice di concentrazione di Bonferroni: