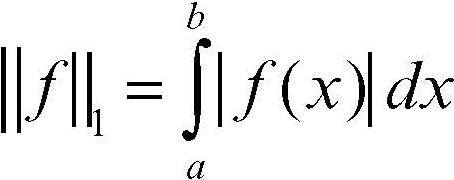completamento

completamento

completamento in analisi, il completamento di uno spazio metrico E è uno spazio Ẽ che contiene un sottospazio E′ isomorfo a E e denso in Ẽ. Per esempio, il completamento di Q è R, l’insieme Q′ essendo formato da quei reali che corrispondono a un numero razionale. La parola completamento indica anche la costruzione di Ẽ a partire da E, costruzione che ripercorre la definizione di numero reale secondo Cantor. Naturalmente se lo spazio è anche vettoriale, tale struttura si mantiene anche nel completamento. Nel caso di spazi normati di dimensione finita il completamento è unico, tuttavia questo non avviene per spazi di dimensione infinita, muniti di norme non equivalenti (in dimensione finita tutte le norme sono equivalenti). Per esempio, lo spazio C⁰([a, b]) è già completo nella norma del massimo

mentre nella norma integrale

non lo è: il suo completamento con tale norma è lo spazio L¹(a, b) delle funzioni integrabili nel senso di Lebesgue (→ Lebesgue, integrale di).

□ In algebra lineare, si dice completamento a base un algoritmo che permette di completare k vettori linearmente indipendenti di uno spazio vettoriale di dimensione n con n − k vettori, in modo da costituire una base dello spazio vettoriale stesso. Il teorema di completamento a base stabilisce che ciò è sempre possibile.