complesso simpliciale
complesso simpliciale
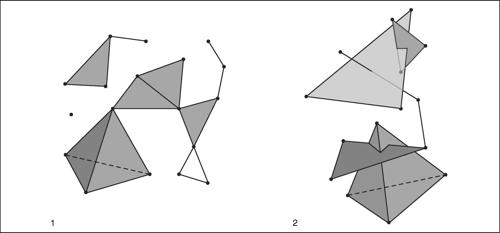
complesso simpliciale nozione fondamentale in topologia combinatoria che generalizza il concetto di superficie triangolata (quale per esempio la superficie di un poliedro). Talvolta si aggiunge l’aggettivo «euclideo» o «geometrico» per evitare la possibile confusione con il concetto di → complesso simpliciale astratto. Un complesso simpliciale finito K di Rn è una famiglia di simplessi euclidei che soddisfa le seguenti proprietà:
a) ogni faccia di un simplesso euclideo di K appartiene a K;
b) l’intersezione di due simplessi euclidei di K è una faccia di entrambi.
Una faccia di dimensione k di un complesso simpliciale K è un qualsiasi simplesso di dimensione k appartenente a K. I vertici del complesso simpliciale K sono i punti che costituiscono le facce di K di dimensione 0. La dimensione di un complesso simpliciale è la massima dimensione dei simplessi euclidei che gli appartengono. Il supporto di un complesso simpliciale K, solitamente indicato con |K|, è lo spazio topologico dato dall’unione di tutti i simplessi in K, con la topologia indotta da Rn.
Un complesso simpliciale infinito K di Rn è una famiglia di simplessi euclidei tale che, oltre a soddisfare le due proprietà a) e b), soddisfa anche la seguente proprietà:
c) per ogni punto p di Rn esiste un intorno di p che interseca solo un numero finito di simplessi di K.
Strettamente collegata alla nozione di complesso simpliciale è quella di triangolazione di uno spazio topologico X (è la coppia formata da un complesso simpliciale K e da un omeomorfismo di |K| su X): mediante l’uso di opportune triangolazioni si analizzano certe proprietà topologiche di un ente continuo (per esempio una superficie) sostituendogli un ente discreto che è possibile studiare secondo i procedimenti sviluppati nell’ambito della topologia combinatoria (→ spazio topologico, triangolazione di uno).