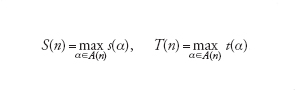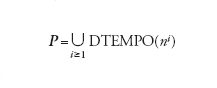Complessità algoritmica

Complessità algoritmica

Gli studi di complessità di calcolo si sono sviluppati essenzialmente nella seconda metà del ventesimo secolo. Basati sulla formalizzazione del concetto di algoritmo, databile ai primi decenni dello stesso secolo, questi studi furono motivati dallo sviluppo dei calcolatori, divenuti in breve tempo così importanti da richiedere un esame approfondito sull'efficienza della computazione.

Il modello teorico classico di algoritmo è la macchina di Turing, equivalente a ogni altro modello ben posto come asserito nella ipotesi di Church. In questa luce a ogni programma di un calcolatore corrisponde una macchina di Turing, ma è anche possibile definirne una universale che simula il comportamento di ogni altra. Dal punto di vista della computazione la macchina universale è equivalente a qualsiasi calcolatore reale.

La descrizione finita di algoritmo (o procedura) implica che la classe di tutti gli algoritmi sia numerabile e da ciò deriva una famosa dimostrazione di esistenza di problemi non calcolabili mediante un algoritmo. Questi argomenti sono studiati in un capitolo della teoria della computazione noto come computabilità. Noi ci riferiremo qui solo a problemi calcolabili, studiandone la complessità secondo precise definizioni matematiche che mettono in relazione le risorse necessarie al calcolo (in particolare il tempo) alla dimensione dei dati del problema. A tale proposito si deve notare che, come la classe degli algoritmi, anche le classi dei dati su cui essi operano e dei risultati che producono sono numerabili. Un algoritmo è quindi un meccanismo di calcolo di una funzione da ℕ su ℕ (cioè dai naturali sui naturali). Lo studio può essere limitato agli algoritmi di decisione che calcolano funzioni da ℕ su {0,1} (decidono se accettare o respingere un'asserzione rappresentata dai dati), se, come in genere accade, tali algoritmi rendono conto della complessità del problema.

Benché possa apparire sorprendente, lo studio di efficienza degli algoritmi ha riscosso attenzione crescente al crescere della velocità e dimensione dei calcolatori, ed è divenuto argomento centrale nella teoria della computazione solo con la nascita di macchine estremamente potenti che parrebbero rendere secondari gli studi sul modo più opportuno di impiegarle. Due motivi hanno invece generato l'effetto contrario. Il primo, abbastanza semplice, è che l'uomo basa oggi il progresso economico e tecnologico sulla risoluzione numerica di problemi così vasti da essere stati ritenuti praticamente non affrontabili prima dell'avvento dei grandi calcolatori. Non vi è però virtualmente limite alle dimensioni dei problemi ancora fuori della portata dei mezzi di calcolo: si tende perciò ad ampliare la potenza delle macchine e a raffinarne le tecniche di impiego.

Il secondo motivo, assai più sottile, è legato ai meccanismi del calcolo non deterministico. La macchina di Turing, nella sua più generale definizione, ha la possibilità di rispondere in modo non deterministico alle stesse condizioni di ingresso, secondo un modello di comportamento definito matematicamente e simulato in pratica con l'esecuzione alternativa di tutte le azioni possibili a ogni passo. Se quindi il non determinismo non amplia la classe delle funzioni calcolabili, esso incide in modo cruciale sul tempo di calcolo, poiché una sequenza di n passi non deterministici ciascuno dei quali preveda m alternative è simulata attraverso mⁿ passi deterministici. Nel decennio tra il 1960 e il 1970 si giunse alla conclusione che la misura più significativa dell'efficienza di un algoritmo è l'espressione matematica del tempo che esso richiede in funzione della dimensione dei dati d'ingresso. Gli algoritmi si divisero in efficienti e inefficienti a seconda che il tempo richiesto fosse polinomiale o esponenziale. In un famoso lavoro del 1971 sulla complessità delle procedure di dimostrazione, Stephen A. Cook provava che tutti i problemi risolubili in tempo polinomiale con una macchina di Turing non deterministica si riducono all'unico problema della soddisfattibilità di espressioni booleane. Negli anni seguenti si riconobbe che numerosissimi problemi ben posti e praticamente rilevanti sono equivalenti dal punto di vista computazionale a quello della soddisfattibilità: esistono cioè algoritmi efficienti per risolverli nel modello non deterministico, ma la pratica simulazione di essi è inefficiente poiché richiede tempo esponenziale. Se d'altra parte si scoprisse un algoritmo polinomiale deterministico per risolvere uno di questi problemi, lo stesso algoritmo sarebbe sufficiente a risolverli tutti in pari tempo.

Notazione

La teoria degli algoritmi è basata su descrizioni finite e discrete, costruite con i caratteri (o simboli ) di un insieme finito Σ detto alfabeto. La notazione di base è quindi quella della teoria degli insiemi con alcune estensioni. Una stringa w su Σ è una sequenza finita di caratteri di Σ; la sua lunghezza ∣w∣ è il numero di caratteri che essa contiene. La stella Σ* di Σ è l'insieme (infinito) di tutte le stringhe sull'alfabeto, inclusa la stringa vuota. Un linguaggio L è un insieme finito o infinito di stringhe su Σ, cioè L∈Σ*.

Posto che con l'alfabeto Σ si rappresentino ogni algoritmo A e i suoi dati d'ingresso e uscita, l'insieme di dati e risultati possibili è Σ*, ovvero A calcola una funzione f da Σ* su Σ*. Indicando con ℕ l'insieme dei numeri naturali e notando che Σ* è ovviamente numerabile, sotto un'arbitraria numerazione delle sue stringhe si può affermare che f è una funzione da ℕ su ℕ, o da ℕ su {0,1} se A è un algoritmo di decisione. In questo caso se L è il sottoinsieme di Σ* per cui A dà risposta 1, diremo che L è il linguaggio accettato da A. La complessità di calcolo è rivolta primariamente allo studio del tempo necessario a tale accettazione.

Algoritmi deterministici e non deterministici

La macchina di Turing è una macchina astratta di dimensioni finite, dotata di una testa che scandisce le celle di un nastro esterno di lunghezza illimitata su cui esegue operazioni di lettura e scrittura e di un controllo che determina, attraverso l'evoluzione tra diversi stati, la sequenza di operazioni relative al problema da risolvere. Nella sua forma di base la macchina rappresenta un algoritmo di risoluzione di un problema specifico su dati d'ingresso rappresentati all'inizio sul nastro. Le condizioni di arresto dipendono dal tipo di algoritmo eseguito. Se è richiesto un risultato più complesso di una semplice decisione, la macchina si arresta quando raggiunge uno stato finale rappresentando il risultato sul nastro. Se la macchina deve risolvere un problema di decisione, come ora vedremo il risultato è indicato dallo stato raggiunto all'arresto. Le principali proprietà della macchina di Turing, e la famiglia di linguaggi che essa riconosce, possono essere approfondite nell'ambito della teoria della computabilità. Ci occupiamo qui invece prevalentemente del numero di mosse che la macchina esegue, che può essere messo in corrispondenza al tempo richiesto da un equivalente programma di un calcolatore.

Formalmente la macchina di Turing corrispondente a un algoritmo di decisione è una collezione di entità (S,s′,Σ,Π,b,F,∂) ove:

S è un insieme finito di stati; s′∈S è lo stato iniziale; Σ è l'alfabeto d'ingresso; Π è l'alfabeto del nastro, Σ⊂Π; b∈Π−Σ è un carattere speciale del nastro, detto bianco; F⊆S è l'insieme di stati finali; ∂ è la funzione di transizione da S×Π su S×Π×{←,→}.

La funzione ∂ può non essere definita sull'intero dominio S×Π e in particolare non è definita su F×Π.

Inizialmente il nastro contiene una stringa d'ingresso α∈Σ* registrata a partire dalla prima cella, seguita da una stringa di b illimitata a destra. La macchina inizia a operare nello stato s′, con la testa posta sulla prima cella del nastro; in ogni istante essa si trova in uno stato s∈S, legge un carattere c∈Π dal nastro ed esegue una delle azioni seguenti:

1) Se ∂(s,c)=(t,d,m), con t∈S, d∈Π, m∈{←,→}, la macchina si porta nello stato t, cancella c dal nastro e scrive al suo posto d, sposta la testa sul nastro di una posizione, a sinistra se m=←, a destra se m=→;

2) Se ∂(s,c) non è definita, o se la testa si sposta a sinistra dell'origine del nastro, la macchina si arresta.

In tal modo la stringa iniziale αbbb… si trasforma a ogni passo in un'altra, composta con i caratteri di Π. La stringa α è accettata, ovvero la risposta è 1, se la macchina si porta in un numero finito di mosse in uno stato f∈F, ove si arresta. La stringa α non è accettata, ovvero la risposta è 0, se la macchina si arresta in uno stato di S−F. La teoria della computabilità insegna che possono esistere stringhe per cui la macchina non si arresta mai. In linea teorica anche queste stringhe non sono accettate, tuttavia la teoria della complessità esclude questo caso limitando lo studio alle macchine di Turing che si arrestano sempre, cui è propriamente assegnato il nome di algoritmi.

Pur essendo un modello utilissimo per studiare problemi di complessità da un punto di vista teorico, la determinazione di una macchina di Turing che risolva un problema dato, anche elementare è in genere molto difficile: in particolare essa può contenere molti stati e la funzione ∂, specificata in genere con una tabella che ne elenca i valori per tutte le coppie stato/carattere, può essere complicata da definire e ardua da interpretare. Asserita l'equivalenza tra macchina di Turing e altri modelli di calcolo, si ricorre quindi alla formulazione degli algoritmi come programmi per un calcolatore astratto, riformulabili immediatamente nel linguaggio accettato da un qualsiasi calcolatore reale. Consideriamo un problema fondamentale:

Problema della soddisfattibilità (P_sod). Data un'arbitraria espressione E costruita sulle variabili logiche x₁,…,x_n con gli operatori , , ⌝, stabilire se esiste un insieme di valori x′₁,…,x′_n tale che E(x′₁,…,x′_n)=true.

Un metodo per risolvere P_sod è quello di generare tutte le possibili n-ple di valori binari per x₁,…,x_n e di valutare E per ciascuna di esse. Ciò è realizzato nel seguente programma di semplice comprensione, in cui le n-ple vengono costruite assegnando in tutti i modi possibili i valori true e false agli elementi V[i ] di un vettore V e controllando, quando ogni n-pla è stata completata (risposta affermativa al test if k=n), se la E è soddisfatta da quei valori e la n-pla è quindi accettata. Si noti la forma ricorsiva della procedura - chiamata di SAT(k+1) all'interno di SAT(k) - innescata all'inizio dalla chiamata SAT(1).

Procedure SAT(k)

for c=true,false

V[k]←c

if k=n then (if E(V[1],…,V[n])=true then accetta)

else SAT(k+1)

Poiché il programma costruisce 2ⁿ configurazioni binarie di n elementi, e per ognuna di essi esegue un numero costante di operazioni tra cui il calcolo di E sulla n-pla è verosimilmente la più costosa, il tempo richiesto è di ordine O(2ⁿ∙t_E), anche se questo concetto sarà affinato nel seguito.

Una possibile estensione è la macchina di Turing non deterministica (MTND) che, per lo stesso stato e lo stesso carattere letto sul nastro, può eseguire più mosse. Il significato di S, Σ, Π, s′, b, F resta invariato, mentre la funzione di transizione è ora definita come ∂′ da S×Π su 2S×Π×{←,→}. Una stringa α è accettata in t mosse se almeno una delle computazioni per α raggiunge uno stato finale, e la più breve tra tali computazioni consiste di t mosse. Nonostante l'apparente potenziamento del modello, la teoria della computabilità dimostra che gli insiemi di stringhe accettate non cambiano, mentre cambia il numero di mosse eseguite dalle due famiglie di macchine. Abbiamo infatti:

Teorema 1. Per ogni MTND X esiste una macchina di Turing Y che accetta esattamente le stesse stringhe, tale che ogni stringa α accettata da X in t mosse è accettata da Y in t′>kt−1 mosse, con k costante.

Ammettendo che ogni mossa sia eseguita in tempo costante, i valori t e t′ del teorema possono essere presi come tempi di esecuzione di due algoritmi, uno deterministico corrispondente a Y e uno non deterministico corrispondente a X, limitati all'insieme delle stringhe accettate. Non si studiano questi tempi per una stringa α non accettata poiché i diversi percorsi di computazione di una MTND richiedono diversi numeri di mosse, e non si può affermare che α non sarà accettata finché non si sono concluse tutte le computazioni.

La dimostrazione del teorema 1 è basata su una simulazione del funzionamento della MTND X sulla macchina di Turing Y, ove il tempo di esecuzione cresce esponenzialmente nel passaggio dalla macchina non deterministica a quella deterministica: è importante però mettere in evidenza che ciò non esclude l'esistenza di una Y′ che accetti lo stesso linguaggio in un tempo inferiore a quello richiesto da Y, e in particolare in un tempo polinomiale in t: quest'ultimo quesito è ancora irrisolto e come vedremo è di cruciale importanza in una discussione generale sulla complessità di calcolo.

Nella formulazione di algoritmi mediante programmi, le MTND sono rappresentate da programmi non deterministici (ND), che prevedono l'esecuzione contemporanea di diverse frasi tutte egualmente accettabili. Questo si ottiene utilizzando costrutti linguistici particolari come choice A, che provoca la scelta non deterministica di tutti gli elementi di un insieme A. Per essere praticamente eseguito, un programma ND X deve essere simulato da un programma deterministico Y che realizza ogni costrutto choice A scegliendo uno a uno in sequenza gli elementi di A. Il rapporto tra i tempi di esecuzione di Y e X è esponenziale come nelle macchine di Turing. I programmi ND si prestano ad affrontare problemi a carattere enumerativo come P_sod, che è risolubile con il semplicissimo programma:

for i=1,2,…,n

V[i ]←choice {true,false}

if E(V[1],…,V[n])=true then accetta else non accetta

La E è soddisfatta se e solo se almeno una delle computazioni termina su accetta. Il tempo di funzionamento del programma nel caso di accettazione è in ordine di grandezza O(n+t_E), ove n è proporzionale al numero di operazioni per generare una n-pla e t_E è il tempo per calcolare il valore di E sulla n-pla stessa. Si noti che la procedura deterministica SAT vista in precedenza simula di fatto il nuovo programma costruendo tutte le n-ple di valori true, false in un ordine assegnato, e calcolando il valore di E per ciascuna di esse. Il tempo richiesto da SAT è di ordine O(2ⁿ∙t_E), e, in accordo con il teorema 1, cresce esponenzialmente rispetto al tempo richiesto dal programma ND.

Complessità in tempo e spazio

Come già detto la teoria della complessità si occupa di problemi risolubili mediante algoritmi. Ognuno di questi problemi, diciamo P, è risolto da una macchina di Turing (deterministica) M che si arresta per ogni istanza di P (algoritmo per P). Lo stesso problema può essere risolto con infiniti algoritmi derivabili per esempio da M con banali aggiunte di mosse inutili ed è ovviamente più interessante considerare quelli fondati su metodi sostanzialmente differenti, per porli a confronto in base alla quantità di risorse richieste. Ciò conduce alle seguenti definizioni.

Nella computazione di M su una stringa d'ingresso α, sia s(α) il numero di celle diverse (oltre quelle contenenti α) visitate sul nastro dalla testa di M e sia t(α) il numero di mosse compiute da M. Considerato, per ogni numero naturale n∈ℕ, l'insieme A(n)={α tali che ∣α∣=n}, si dice che M ha complessità in spazio S(n) e complessità in tempo T(n) ponendo:

[1]  formula.

Per ogni valore di n, la complessità di M in spazio e tempo si valuta dunque per la stringa α che corrisponde al caso pessimo, e costituisce un limite superiore alla complessità del problema poiché garantisce che P può essere sempre risolto entro i valori S(n) e T(n) utilizzando M. Si dichiara quindi che anche P ha complessità S(n) e T(n), senza escludere l'esistenza di una diversa macchina di Turing M′ che risolva P con complessità inferiori: la scoperta di una tale M′ consentirebbe di aggiornare le complessità dichiarata per P.

Definiamo ora le classi di complessità DSPAZIO(S(n)) e DTEMPO(T(n)) come le classi di tutti i problemi che hanno rispettivamente complessità in spazio minore o uguale S(n) e complessità in tempo minore o uguale T(n), dove l'iniziale D indica che la macchina di Turing risolvente è deterministica. Tutte le funzioni f(n) citate nel seguito sono per ipotesi funzioni calcolabili, cioè per ogni n esiste un algoritmo per calcolare il valore di f(n). Abbiamo:

Teorema 2. Per ogni funzione f(n) esiste almeno un problema P tale che P∉DSPAZIO(f(n)) e P∉DTEMPO(f(n)).

Teorema 3. Per ogni problema P esiste una costante c tale che: 1) se P∈DTEMPO(f(n)) allora P∈DSPAZIO(cf(n)); 2) se P∈DSPAZIO(f(n)) e f(n)≥log₂ allora P∈DTEMPO(c^f(n)).

Il teorema 3 mostra che la complessità in tempo è parametro più critico di quella in spazio, poiché può crescere esponenzialmente rispetto a quest'ultima. Approfondiremo quindi nel seguito lo studio della complessità in tempo T(n), detta semplicemente complessità quando tale dizione non sia ambigua, ricordando che esistono studi paralleli sulla complessità in spazio. Si dice che una macchina di Turing (o un algoritmo) M è polinomiale se esiste un polinomio p tale che, per ogni valore di n, sia T(n)≤p(n) o, in modo equivalente, se il problema P risolto da M appartiene a DTEMPO(p(n)). Ciò conduce alla definizione della classe P dei problemi risolubili in tempo polinomiale, ovvero risolubili efficientemente:

[2] formula

I concetti esposti si estendono alle MTND M e ai problemi P che esse risolvono, con una dissimmetria di funzionamento per le stringhe accettate e non accettate. Per una stringa d'ingresso α accettata da M, s(α) è il minimo numero di celle diverse visitate sul nastro oltre quelle contenenti α, calcolato ora su tutte le computazioni di M a causa del non determinismo; t(α) è invece il numero di mosse della computazione più breve. Se α non è accettata da M si pone convenzionalmente s(α)=t(α)=1. Le complessità in spazio e tempo S(n) e T(n) per M e P si definiscono esattamente come per le macchine di Turing ordinarie impiegando i nuovi valori di s(α) e t(α) e le corrispondenti classi di complessità dei problemi si indicano con NDSPAZIO(S(n)) e NDTEMPO(T(n)). Per quanto concerne la complessità in tempo, vale la seguente relazione tra le classi deterministiche e non deterministiche:

Teorema 4. Per un arbitrario problema P esiste una costante c tale che se P∈NDTEMPO(f(n)) allora P∈DTEMPO(c ^f(n)).

Anche nel caso non deterministico una MTND (o un algoritmo ND) M è detta polinomiale se esiste un polinomio p tale che, per ogni valore di n, sia T(n)≤p(n). Ciò conduce alla definizione della classe NP dei problemi per i quali esiste una MTND polinomiale che li risolve:

[3] formula.

Poiché possiamo considerare una macchina di Turing come MTND che non presenta mai scelte multiple,dalle definizioni di P e NP segue la relazione P⊆NP.Non esiste però alcuna prova che P≠NP, benché ciò sia normalmente ritenuto vero a causa dell'abilità delle MTND polinomiali di eseguire un numero esponenziale di computazioni in tempo polinomiale e della nostra ignoranza su un modo di ottenere gli stessi risultati con una macchina di Turing ordinaria.

Problemi intrattabili

Studiamo ora gli algoritmi realizzati come programmi di un calcolatore. Nella misura di complessità la variabile n rappresenta lo spazio di memoria occupato dai dati d'ingresso o un numero proporzionale a esso. Le funzioni S(n) e T(n), complessità in spazio e in tempo del programma, indicano rispettivamente il massimo spazio di memoria occupato durante la computazione e il numero di operazioni elementari richiesto; quest'ultimo è proporzionale al tempo di esecuzione del programma se si ammette che ogni operazione richieda tempo costante. S(n) e T(n) si studiano quindi in ordine di grandezza, che permette di considerare tali funzioni come rappresentative dell'algoritmo prescelto indipendentemente dal particolare calcolatore o linguaggio di programmazione impiegato.

Come per le macchina di Turing limiteremo lo studio alla funzione T(n), detta anche semplicemente complessità. Pur misurando la complessità in ordine di grandezza, le classi P e NP conservano il loro significato e restano valide le considerazioni fatte sulla loro relazione. In particolare, ricordando che i programmi non deterministici vengono simulati con programmi deterministici, P è la classe dei problemi effettivamente risolubili in tempo polinomiale.

I problemi non appartenenti a P, per cui esistono o sono noti solo algoritmi deterministici di complessità esponenziale, sono invece detti intrattabili, poiché il tempo richiesto per calcolare la soluzione cresce smisuratamente al crescere di n.

Ovviamente anche un algoritmo polinomiale di grado molto elevato può richiedere un tempo inaccettabile al crescere di n, ma l'esistenza di un tale algoritmo autorizza a mantenere il problema tra quelli per cui vi è almeno speranza di soluzione futura, per il seguente non ovvio motivo. Poniamo che un algoritmo di complessità polinomiale T(n)=n^c e uno di complessità esponenziale T(n)=cⁿ possano essere praticamente risolti fino a un certo valore di n su un calcolatore disponibile, e studiamo come cresce questo valore se si impiega un calcolatore più veloce. Detto m il nuovo valore trattabile in pari tempo di calcolo, e osservando che impiegare un calcolatore k volte più veloce equivale a impiegare il calcolatore originale per un tempo k volte maggiore, abbiamo per l'algoritmo polinomiale m^c=kn^c, ovvero m=k^1/cn: un incremento sensibile, benché percentualmente decrescente al crescere del grado c del polinomio. Per l'algoritmo esponenziale abbiamo invece c^m=kcⁿ, e cioè m=log_ck+n, corrispondente a un incremento trascurabile. Concludiamo che gli algoritmi di complessità esponenziale non traggono alcun giovamento dai progressi tecnologici dei calcolatori e rimangono inevitabilmente inefficienti.

Benché sia possibile dimostrare che tra i problemi intrattabili alcuni sono sicuramente tali poiché richiedono tempo esponenziale anche in un modello di calcolo non deterministico, quasi tutti i casi interessanti appartengono a NP: non si conosce alcun algoritmo polinomiale deterministico per risolverli, ma non vi è prova che tale algoritmo non esista. Per un problema decisionale P, il linguaggio relativo a P è l'insieme L⊆Σ* di tutte le stringhe accettate da una macchina di Turing, o algoritmo, che risolve P. Il meccanismo di base per indagare sui problemi intrattabili è la riduzione: presi due problemi P₁, P₂ e i relativi linguaggi L₁, L₂ , una riduzione polinomiale da P₁ a P² è una funzione f da Σ* su Σ* tale che: 1) esiste un algoritmo polinomiale deterministico F che calcola f; 2) per ogni v∈Σ*, si ha v∈L1 se e solo se f(v)∈L2. Si dice allora che P₁ si riduce a P₂, e si indica con P₁⇒P₂. Si noti che la riduzione polinomiale è transitiva, cioè P₁⇒P₂ e P₂⇒P₃ implicano P₁⇒P₃.

Se P₁⇒P₂, un algoritmo A₂ per risolvere P₂ può essere usato per risolvere P₁ attraverso le computazioni successive di F su v, e di A2 su f(v). Poiché F è polinomiale la computazione complessiva ha la complessità di A₂ e dunque P₂∈P implica P₁∈P, mentre P₂∈NP implica P₁∈NP pur senza escludere che esista un algoritmo polinomiale deterministico per P₁: questa situazione si descrive dicendo che P₂ è difficile almeno quanto P₁. Se P₁⇒P₂ e P₂⇒P₁ i due problemi sono polinomialmente equivalenti.

Se tutti i problemi della classe NP si riducessero a uno solo, questo sarebbe il più difficile problema di tale classe e quindi il primo candidato a trovarsi in NP−''P qualora N≠NP. Formalmente un problema P si dice NP-completo se P∈NP e per ogni altro problema P′∈NP si ha P′⇒P. I problemi NP-completi sono dunque i più difficili problemi in NP, e sono tutti polinomialmente equivalenti. Il primo individuato tra questi è il già citato problema della soddisfattibilità P_sod. Stephen A. Cook ha infatti dimostrato il seguente

Teorema 5. P_sod è NP-completo.

Poiché i problemi NP-completi sono polinomialmente equivalenti, l'esistenza di un algoritmo polinomiale deterministico per risolverne uno implicherebbe che tutti i problemi in NP potrebbero esserlo in pari tempo. Si avrebbe allora P=NP. Il fatto che tanti studi sull'argomento abbiano prodotto solo algoritmi esponenziali conforta la congettura che P≠NP, ma la prova che tale affermazione sia vera o falsa, decidibile o indecidibile non sembra vicina.

La scoperta che P_sod è NP-completo ha permesso di dimostrare che altri problemi P∈NP hanno questa proprietà provando che P_sod⇒P. La classe dei problemi NP-completi contiene oggi, oltre a P_sod, un grandissimo numero di problemi nati in campi diversi. Ne citiamo qui tre di particolare importanza:

Problema del ciclo hamiltoniano (P_ham). Dato un grafo G di n vertici stabilire se esiste in G un ciclo che attraversa tutti i vertici esattamente una volta.

Problema delle scatole (P_sca). Dato un insieme A di n interi positivi e due interi positivi h e k, stabilire se esiste una partizione di A in k sottoinsiemi tale che la somma degli elementi in ogni sottoinsieme sia minore o ugale a h.

Problema delle equazioni diofantine quadratiche (P_edq). Dati tre interi positivi a, b, c di n cifre, stabilire se l'equazione ax²+by+c=0 ha radici intere.

P_ham, P_sca e P_edq sono rispettivamente i capostipiti in forma decisionale dei problemi di percorsi su grafi, di allocazione in una o più dimensioni e di risoluzione intera di equazioni. Se si passa a una più generale forma risolvente chiedendo che si generi una soluzione per tali problemi, essi diventano difficili almeno quanto i corrispondenti problemi decisionali e restano pertanto intrattabili.

Algoritmi randomizzati

Iproblemi che richiedono tempo esponenziale sono numerosissimi e molti di essi hanno grande importanza pratica. A causa dell'impossibilità di risolverli esattamente in tempo ragionevole sono state esplorate nuove vie di soluzione che richiedono tempo polinomiale deterministico, rinunciando all'assoluta certezza che il risultato sia corretto. Si è così sviluppata la teoria degli algoritmi approssimati, in cui le soluzioni si ottengono con preassegnata approssimazione, e quella degli algoritmi randomizzati, le cui soluzioni sono corrette con preassegnata probabilità. Questi ultimi utilizzano come costituente interno un generatore casuale che dovrebbe consentire scelte perfettamente a caso. In pratica si tratta un programma, detto generatore pseudo-casuale, disponibile in ogni sistema di programmazione, le cui uscite hanno una distribuzione con caratteristiche statistiche sufficienti per le necessità dell'algoritmo. Vi sono due modi completamente diversi di sfruttare l'intervento del caso nel calcolo. Il primo, su cui è basato per esempio un famoso metodo di ordinamento, esamina i dati in ordine parzialmente casuale per contrastare situazioni sfavorevoli in cui possono presentarsi. Il tempo di risoluzione del problema risulta così probabilmente basso e il risultato comunque esatto, ma la procedura può essere inefficiente nel caso pessimo. Il secondo metodo è molto più interessante poiché consente di affrontare problemi esponenziali: gli algoritmi che ne derivano, detti appunto randomizzati, generano soluzioni probabilmente corrette in tempo sicuramente breve. Non vi è in questo approccio alcun tentativo di approssimazione della soluzione (nel caso di problemi di decisione, per esempio, una soluzione non corretta è completamente errata), ma gli algoritmi randomizzati sono organizzati in modo che la probabilità di errore sia arbitrariamente piccola, in misura stabilita a priori.

Presenteremo ora lo schema del primo algoritmo randomizzato proposto per decidere se un numero intero N è (probabilmente) primo. Il calcolo utilizza un predicato Z(N,R), cioè una funzione che può valere true o false, basato su alcune complesse proprietà dei numeri primi che non è qui il caso di esporre. Le variabili in gioco sono il numero N di cui si deve stabilire la natura e un secondo numero R indipendente da N ed estratto a caso. Come dimostrato da Gary L. Miller e Michael O. Rabin, si ha:

esiste un predicato Z(N,R), con 2〈R〈N, tale che se N è primo allora Z(N,R)=true per ogni valore di R, e se N è composto allora Z(N,R)=true per un numero di valori di R minore di N/4.

Naturalmente il lemma originale specifica l'espressione di Z(N,R), mostrando che il calcolo del predicato può essere eseguito in tempo polinomiale. Si estrae dunque a caso un intero R e si applica il predicato: se risulta Z(N,R)=false, N è certamente composto; se risulta Z(N,R)=true, N è composto con probabilità minore di 1/4, cioè è primo con probabilità di errore minore di 1/4. Naturalmente questa probabilità è ancora troppo alta per poter accettare N come primo, ma se si estrae a caso un secondo valore di R e il predicato risulta nuovamente vero la probabilità di errore diviene minore di 1/16. Se si ripete il procedimento per un numero prefissato k di volte e si ottiene sempre predicato vero, la probabilità di errore nel dichiarare N primo è maggiorata da 1/4^k ed è cioè inferiore anche per valori di k ragionevolmente piccolia quella che si sia verificato un errore per qualsiasi altra ragione (per esempio se k=15 è minore di uno su un miliardo). Se invece una delle prove indica che il predicato è falso, si arresta il procedimento dichiarando che N è composto. Lo schema di calcolo è il seguente:

for i=1,2,…,k

estrai a caso R, con 2〈R〈N

if Z(N,R)=false then

dichiara N composto con probabilità 1

dichiara N primo con probabilità >1−1/4^k

Questo meccanismo di calcolo dà luogo alla classe di complessità RP dei problemi che possono essere risolti in tempo polinomiale randomizzato, cioè con probabilità di errore prefissata ed esponenzialmente piccola. La relazione tra le principali classi di complessità è P⊆RP⊆NP e si ritiene che non sia verificata l'uguaglianza.

Bibliografia

Aho 1974: Aho, Alfred V. - Hopcroft, John E. - Ullman, Jeffrey D., The design and analysis of computer algorithms, Reading, Addison-Wesley, 1974.

Cormen 1990: Cormen, Thomas H. - Leiserson, Charles E. - Rivest, Ronald L., Introduction to algorithms, Cambridge (Mass.), MIT Press, 1990.

Crescenzi 2006: Crescenzi, Pierluigi - Gambosi, Giorgio - Grossi, Roberto, Strutture di dati e algoritmi, Milano, Pearson Education Italia, 2006.

Davis, Weyuker 1983: Davis, Martin - Weyuker, Elaine, Computability, complexity and languages, New York, Academic Press, 1983.

Demetrescu 2004: Demetrescu, Camil - Finocchi, Irene - Italiano, Giuseppe F., Algoritmi e strutture di dati, Milano, McGraw-Hill, 2004.

Hopcroft, Ullman 1979: Hopcroft, John E. - Ullman, Jeffrey D., Introduction to automata theory, languages and computation, Reading (Mass.), Addison-Wesley, 1979.

Kleinberg, Tardos 2006: Kleinberg, Jon - Tardos, Eva, Algorithm design, Boston, Pearson, Addison-Wesley, 2006.

Lewis, Papadimitrou 1981: Lewis, Harry R. - Papadimitriou, Christos H., Elements of the theory of computation, Englewood Cliffs (N.J.), Prentice-Hall, 1981.

Luccio 1982: Luccio, Fabrizio, La struttura degli algoritmi, Torino, Boringhieri, 1982.

Motwani, Raghavan 1995: Motwani, Rajeev - Raghavan, Prabhakar, Randomized algorithms, Cambridge, Cambridge University Press, 1995.

Salomaa 1985: Salomaa, Arto, Computation and automata, Cambridge, Cambridge University Press, 1985.