commesso viaggiatore, problema del

commesso viaggiatore, problema del

commesso viaggiatore, problema del (in inglese Travelling Salesman Problem, o più brevemente tsp) problema che consiste nella ricerca su un grafo di un particolare ciclo hamiltoniano che rende minimo un determinato parametro. Il problema è proposto come ricerca del percorso di minimo costo in un insieme di città e di vie di comunicazione che le collegano, rappresentate rispettivamente come nodi e archi di un grafo; assegnato a ciascun arco un costo di percorrenza, si chiede di trovare il ciclo hamiltoniano di costo complessivo minimo. Il “costo” del percorso indica un criterio qualsiasi in base al quale è assegnato a ciascun arco un proprio peso: il problema può essere formulato interpretando il peso come lunghezza di ciascun collegamento o come indicatore di traffico, costo autostradale o altro; la soluzione del problema è un percorso chiuso che tocchi una sola volta tutti i nodi e tale che il peso complessivo sia minimo.

Per esempio, nel seguente grafo sono indicati quattro nodi A, B, C e D e sui collegamenti tra essi sono indicati i rispettivi pesi:

Un possibile ciclo hamiltoniano di lunghezza 7 è A, C, B, D, A:

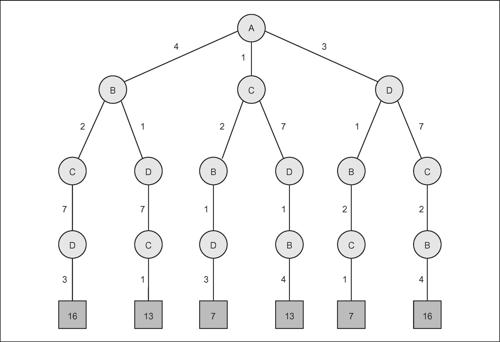
È una soluzione del problema perché la somma minima dei pesi è 7, come si evince dal corrispondente albero che descrive tutti i possibili percorsi di ricerca.

Un altro ciclo hamiltoniano di lunghezza 7 è dato da A, D, B, C, A. L’algoritmo per la risoluzione del problema è un cosiddetto algoritmo a esaurimento perché deve esaminare tutte le possibili scelte: le successioni di scelte via via costruite sono successioni di nodi adiacenti diversi tra loro; la successione è un ciclo hamiltoniano se contiene tutti i nodi del grafo e l’ultimo nodo coincide con il primo; tra questi va poi scelto quello o quelli di peso minimo. La ricerca dei cicli hamiltoniani attraverso tutte le possibili permutazioni dei nodi del grafo può essere realizzata attraverso una procedura ricorsiva; è una ricerca esaustiva, ma può richiedere enormi risorse in termini di tempo di calcolo. Si dimostra che si può tuttavia evitare l’esplorazione di tutte le soluzioni: per esempio, si può abbandonare l’esplorazione di una soluzione prima di terminare il percorso da essa individuato, non appena la somma dei pesi è maggiore di un’altra trovata precedentemente.