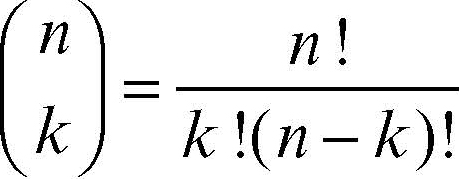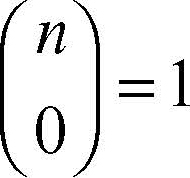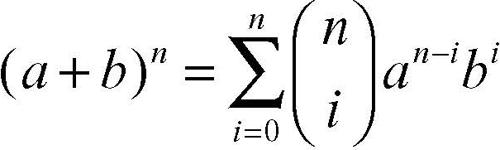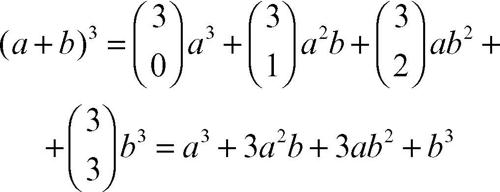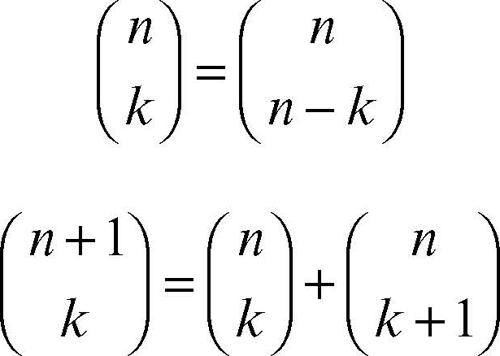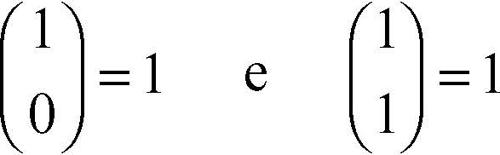coefficiente binomiale
coefficiente binomiale
coefficiente binomiale dati due numeri naturali k, n, con k ≤ n e n ≠ 0, il coefficiente binomiale, indicato con il simbolo
che si legge «n sopra k», è il numero naturale così definito:
dove il punto esclamativo indica il fattoriale del numero; tenuto conto che 0! = 1 per k = 0 si ha
Il nome dipende dal fatto che i suoi valori, per k variabile da 0 a n, sono i coefficienti numerici dello sviluppo della potenza ennesima del binomio (a + b)n. Infatti:
Per esempio:
Valgono le seguenti proprietà:
Da questa seconda proprietà si desume che tutti i suoi valori possono essere ricavati iterativamente a partire da
secondo uno schema chiamato triangolo di → Tartaglia. Il coefficiente binomiale fornisce il numero dei sottoinsiemi con k elementi di un insieme finito costituito da n elementi, numero che d’altra parte coincide con il numero di → combinazioni semplici di classe k di un insieme di n elementi.