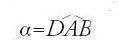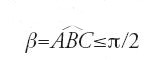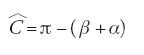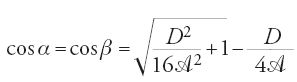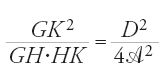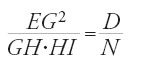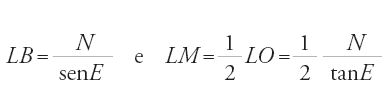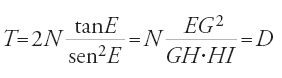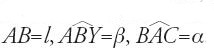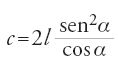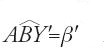Civiltà islamica: antiche e nuove tradizioni in matematica. Tracciato continuo delle coniche e classificazione delle curve

Civilta islamica: antiche e nuove tradizioni in matematica. Tracciato continuo delle coniche e classificazione delle curve

Tracciato continuo delle coniche e classificazione delle curve

Il tracciato continuo delle coniche richiede sia l'invenzione di uno strumento, o di un qualche sistema meccanico, in grado di disegnare queste curve, sia l'elaborazione di concetti della teoria delle coniche suscettibili di spiegare e di controllare l'uso di tale strumento. è una ricerca nella quale si trovano intimamente legate una technè e una théoria, e in questo senso non ha niente a che vedere con un'altra ricerca che ha uno scopo essenzialmente pratico e che richiede solo di trovare lo strumento. Come esempio di quest'ultima ricordiamo la "riga che si incurva", utilizzata da Diocle per unire i punti di un arco di cissoide (Rashed 2000a, p. 84 e p. 133). Si tratta invece questa volta di intraprendere un lavoro concettuale per spiegare la struttura e il funzionamento di un dato strumento. Bisognerà però attendere la seconda metà, se non l'ultimo terzo, del X sec., prima di incontrare questa ricerca matematica sugli strumenti con cui tracciare le curve, e di assistere così alla nascita di un nuovo capitolo delle geometria la cui importanza ed esistenza sono sfuggite agli storici. Un fatto tanto più sorprendente in quanto non si trova niente di simile prima di quest'epoca nella storia della matematica. Era già successo che alcuni tecnici avessero affrontato più o meno direttamente il problema del tracciato continuo delle coniche, ma senza mai farne, per quanto ne sappiamo, la teoria matematica. Si richiamava semplicemente un procedimento senza affrontare la ricerca geometrica in grado di spiegarne la costruzione e l'uso. Le conoscenze che abbiamo della storia del tracciato continuo prima della matematica araba si riducono a un fatto singolare e a un frammento, entrambi risalenti a ingegneri del VI secolo. Sappiamo che Antemio di Tralle tracciava l'ellisse con il metodo 'del giardiniere', che consiste in un movimento continuo ottenuto con un filo le cui estremità sono fissate ai fuochi e che viene tenuto teso da uno stiletto che traccia la curva. Il metodo si basa sulla proprietà seguente: la somma delle distanze dei punti dell'ellisse dai fuochi è costante, ed è uguale alla lunghezza dell'asse maggiore (Rashed 1997, pp. 678-679, 2000a, p. 250 e p. 292). Il frammento è invece una frase, di dubbia autenticità, attribuita a Eutocio, nella quale si afferma che Isidoro di Mileto (Tannery 1884) aveva inventato uno strumento per tracciare la parabola. Ricordiamo questa frase: "La parabola si traccia mediante uno strumento inventato dal nostro maestro Isidoro il meccanico, di Mileto, e da lui descritto nel commento al trattato di Erone dal titolo Sui forni (ϰαμαϱιϰῶν)" (Eutocio, commento a Della sfera e del cilindro di Archimede, IV, p. 62). Non è certo, ma stando al nome (διαβήτηϚ) questo strumen to era apparentemente un compasso. Ora questa stessa frase è presente anche nella traduzione araba del commento di Eu tocio che il matematico al-Qūhī conosceva. Questi, che per primo scrisse su tale tipo di compasso, non cita questa affermazione, ma dichiara al contrario che niente di simile ci è giunto in materia dagli Antichi. Il suo giovane contemporaneo al-Siǧzī, incline all'erudizione, ricostruisce una storia un po' leggendaria del 'compasso perfetto', partendo manifestamente dalla frase attribuita a Eutocio; senza altre informazioni di carattere storico o linguistico interpreta διαβήτηϚ come questo 'compasso perfetto'. Tutto quel che si può dire è che se gli ingegneri bizantini Antemio e Isidoro nel corso della loro attività pratica sono stati posti di fronte al problema del tracciato continuo, non l'hanno affrontato per le tre curve insieme, né hanno elaborato una teoria geometrica dello strumento.

Tutto sta dunque a indicare che se i matematici greci hanno incontrato il problema del tracciato continuo non l'hanno mai considerato un tema di ricerca. Una situazione che ritroviamo ancora tra i matematici arabi fino alla metà del X secolo. Vi sono certamente studiosi, come Ibn Sinān (296/909-335/946), che iniziano le ricerche sulla costruzione per punti (Rashed 2000c, p. 245 e segg.), ma non ancora sul tracciato continuo. Quest'ultimo tema di ricerca si imporrà all'attenzione qualche decennio dopo. Si assisterà infatti a opera di tre dei successori di Ibn Sinān, e dei più prestigiosi, all'invenzione di nuovi strumenti per il tracciato continuo e all'elaborazione dei mezzi teorici necessari a stabilirlo. Si tratta di al-Qūhī, nel Kitāb fī 'l-birkār al-tāmm (Libro sul compasso perfetto) (Woepcke 1874; Rashed 1993, 2003a), di Ibn Sahl nel Kitāb al-Ḥarrāqāt (Libro degli strumenti ustori) (Rashed 1990, 1993) e di al-Siǧzī in un breve trattato che abbiamo appena scoperto, dal titolo Risāla fī ῾amal al-birkār al-tāmm (Epistola sulla costruzione del compasso perfetto) (Rashed 2003b).

Che nello stesso periodo tre matematici di primo piano si siano interessati al medesimo problema è un fatto che merita di essere descritto e analizzato. Mentre Ibn Sahl concepisce un sistema meccanico basato sulle proprietà dei fuochi e della direttrice per tracciare le tre sezioni coniche, e solo queste, al-Qūhī inventa il compasso perfetto per tracciare tutte le linee che egli chiama, come vedremo, 'misurabili', qiyāsiyya, cioè le tre coniche, ma anche il cerchio e la retta. Quanto ad al-Siǧzī, egli intende perfezionare questo strumento per tracciare anche sezioni simili.

Questi tre matematici costituiranno perciò, insieme ma con ruoli diversi, il nucleo di una nuova tradizione di ricerca che proseguirà per due secoli. L'importanza di questo fatto, come pure il ruolo di fondatore di al-Qūhī, non sono certo sfuggiti agli immediati successori. Al-Bīrūnī (973-dopo il 1050) nel Fī istī῾āb al-wuǧūh al-mumkina fī ṣan῾at al-aṣṭurlāb (Su tutti i possibili metodi per la costruzione dell'astrolabio) scrive:

Un gruppo di eminenti matematici moderni, come Ibrāhīm ibn Sinān, Abū ǧa῾far al-Ḫāzin e molti altri, si sono impegnati a tracciare le sezioni coniche dopo quanto Apollonio ha esposto nel libro delle Coniche. Ciascuno di loro cerca di determinare uno dopo l'altro i punti sulle curve. Abū Sahl Wayǧan ibn Rustam al-Qūhī ha invece scritto un libro per tracciarle con il compasso perfetto. Lo chiama 'perfetto' per via della possibilità che offre di costruire la linea retta e la linea circolare e tutte e tre le sezioni coniche, una costruzione effettiva, che non richiede di dover unire e aumentare più punti sulle curve. (Ms. Leida Or. 591, f. 148)

Questi tre matematici inaugurano quindi effettivamente una tradizione di ricerca, nella quale altri poi si inseriranno; è il caso di Ibn al-Hayṯam, al-Bīrūnī, Hibat Allāh al-Baġdādī, Muḥammad ibn al-Ḥusayn (Rashed 2003a).

Si tratta ora di capire per quale motivo il problema del tracciato continuo delle coniche si sia posto nella seconda metà del X sec. e non prima, con tale forza che molti matematici, e non dei minori, si sono impegnati a risolverlo. Il motivo vero sta nelle nuove direzioni prese dalla ricerca matematica araba nei secc. IX e X. Ricordiamone rapidamente qualcuna, assieme ad alcuni capitoli di matematica che hanno imposto il tema del tracciato continuo.

Il primo capitolo è quello delle costruzioni geometriche attraverso l'intersezione di coniche (Rashed 2000b). Non si tratta più come nella vecchia geometria, quella di Eutocio per esempio, di problemi isolati, nati in modo sporadico e risolti poi ricorrendo all'intersezione di curve, coniche o altro. Ora si dispone di un metodo per esplorare il campo dei problemi geometrici, in grande maggioranza problemi solidi, ma eventualmente, e inutilmente possiamo dire, anche piani, che è basato sulle sole coniche escludendo tutte le altre curve. Nell'ambito di questo nuovo capitolo alcuni matematici studiano, di solito anche accuratamente, l'esistenza di soluzioni e il numero di queste. Condotto attraverso l'analisi e la sintesi, questo studio si basa sulle proprietà asintotiche e locali delle coniche, e in particolare sul loro contatto. Coltivato dai matematici a partire dalla metà del IX sec., questo nuovo capitolo diventa un campo di ricerca attivo per opera di matematici della seconda metà del X sec., cioè al-Qūhī, Ibn Sahl, al-Siǧzī, Abū al-ǧūd, ecc. Con essi, la costruzione per mezzo delle sezioni coniche diventa ammissibile in geometria allo stesso titolo di quella con riga e compasso. Inoltre questi stessi geometri che nel corso delle costruzioni procedevano per trasformazioni geometriche ‒ similitudini, traslazioni, omotetie, affinità ‒ introducono i movimenti sia negli enunciati sia nelle dimostrazioni (Rashed 2000b, 2002). Questi movimenti continui ‒ spostamenti, rotazioni ‒ sono sempre realizzati con il supporto di questo o di quello strumento e sono ogni volta esattamente riproducibili. Era evidentemente necessario affrontare lo studio teorico e pratico dei metodi per riprodurre questi movimenti e tracciare quindi le coniche. È quanto fu fatto.

Il capitolo riguardante le costruzioni non era però il solo che richiedesse uno studio di questo tipo. Effettivamente in questo periodo si cominciano a risolvere alcune equazioni cubiche attraverso l'intersezione di coniche. Anche qui bisognava generare la curva mediante un movimento per assicurarne la continuità, nozione quest'ultima ormai fondamentale per la discussione del problema dell'esistenza dei punti di intersezione delle curve.

Tuttavia oltre a questi orientamenti interni alla ricerca geometrica e all'elaborazione di questi nuovi capitoli della geometria, intervengono anche le esigenze delle nuove acquisizioni della matematica applicata: lo studio sistematico degli specchi ustori (parabolici, ellissoidali) e delle lenti piano-convesse e biconvesse da parte di Ibn Sahl, come pure le proprietà anaclastiche delle tre coniche, la ricerca teorico-pratica sugli astrolabi e sui quadranti solari (Rashed 2000c). A dire il vero, non è un effetto del caso se Ibn Sahl e al-Qūhī so no stati i primi a concepire questo nuovo capitolo sul tracciato continuo. Non è forse Ibn Sahl il primo a elaborare una teoria geometrica degli strumenti ustori, cioè degli specchi e delle lenti? Non è forse al-Qūhī che scrive il primo libro dedicato alla geometria dell'astrolabio? E non sono loro i due matematici all'avanguardia della ricerca sulla teoria delle coniche e sulle sue applicazioni? Dobbiamo perciò soffermarci sui loro scritti.

Ibn Sahl: un dispositivo meccanico per tracciare le sezioni coniche

Nel Kitāb al-Ḥarrāqāt (Rashed 1990, 1993) Ibn Sahl prende le mosse dalle proprietà del fuoco e della direttrice per ideare un apparecchio per il tracciato continuo. L'apparecchio è composto di due parti: una non è deformabile, l'altra lo è, senza però cambiare di lunghezza. La prima parte è costituita da righe rigide e da pulegge, la seconda da una cinghia o da un filo deformabile che può prendere varie forme sempre conservando una lunghezza costante. La cinghia si avvolge sulle pulegge, che hanno la funzione di impedirne la rottura. A ciò si aggiunge uno stiletto posto al centro di una puleggia mobile che traccerà la curva richiesta.

Così, per tracciare un arco di parabola AB, di fuoco F e direttrice D, Ibn Sahl immagina un dispositivo composto da una riga che funge da direttrice, una squadra di lunghezza costante HH′=l, dove H è il vertice dell'angolo retto della squadra, e H′ sta sulla riga. Quando la squadra scorre sulla riga, H descrive una retta Δ che è perpendicolare all'asse della sezione. Nel punto H si fissa, dunque, l'estremità di una cinghia che è deformabile senza cambiare lunghezza. In un punto M di HH′ si pone una puleggia mobile e in F una puleggia fissa sulla quale si dispone l'altra estremità della cinghia.

Quest'ultima deve essere mantenuta tesa con uno stiletto posto in M. Ibn Sahl dimostra allora che se M è tale che MF=MH′, allora M è il punto corrente della parabola. In effetti esso soddisfa MF+MH=l.

Nel caso dell'ellisse, la lunghezza fissa l è quella dell'asse maggiore, mentre F e F′ sono i due fuochi. Il dispositivo proposto questa volta da Ibn Sahl differisce dal famoso metodo del 'giardiniere' soltanto perché si serve di tre pulegge, due nei fuochi e una nel punto mobile M. La cinghia di lunghezza l si avvolge sulla puleggia M e le sue estremità sono fissate nella pulegge F e F′. Il punto M è il punto corrente dell'ellisse; soddisfa infatti MF+MF′=l.

Infine, per tracciare l'iperbole di fuochi F e F′ e di asse trasverso 2a Ibn Sahl immagina un dispositivo formato da due righe e due pulegge. La prima riga FF′ è fissa, la seconda FS è mobile e ruota attorno al fuoco F. Considera poi una cinghia con un'estremità su una puleggia fissa posta in F′ e l'altra in un punto S della riga mobile. Intorno a questa puleggia si fa passare la cinghia che deve essere tenuta tesa per mezzo di uno stiletto che poggia sulla riga in M.

Se ora FS=l, lunghezza costante, la lunghezza della cinghia sarà l′=l+2a. In questo caso la punta dello stiletto traccia l'iperbole MB quando la riga ruota attorno a F. In effetti, il punto M soddisfa in questo caso MF′−MF=2a, da cui (SM+MF′)−SF=2a.

Al-Qūhī: il compasso perfetto

Al-Qūhī, contemporaneo di Ibn Sahl, concepisce un altro strumento che permette il tracciato continuo delle coniche, ma anche del cerchio e delle rette. È grazie a questo strumento che è facile, egli scrive, "costruire astrolabi su superfici piane o superfici di rivoluzione, come pure quadranti solari su una superficie qualunque, ma anche tutti gli strumenti sui quali si trovano le linee intersezione di una superficie conica con una superficie qualunque" (Rashed, 2003a). A questo compasso al-Qūhī dedica un intero trattato geometrico in due libri: nel primo elabora una teoria dello strumento, nel secondo passa alle applicazioni. Osserviamo che, nonostante le dichiarazioni preliminari sull'utilità di questo strumento per astrolabi, quadranti, ecc., tutte le applicazioni contenute nel Libro II sono puramente geometriche.

Il Libro I del trattato comincia con la descrizione del compasso perfetto e prosegue con le istruzioni su come usarlo per tracciare in un piano dato le varie curve: retta, cerchio, parabola, ellisse, iperbole (uno o due rami).

Il compasso perfetto è composto da quattro parti articolate:

a) una parte piana che ne costituisce la base e che contiene la 'retta del centro' AD;

b) l''asse del compasso' AB che può ruotare attorno al punto A detto 'centro', sempre restando nel piano Q perpendico lare al piano P lungo la retta AD; la sua posizione è determinata dall'angolo al centro del compasso

c) la 'retta del vertice' BC, che può ruotare attorno al punto B detto 'vertice'. Se ne considera dapprima la posizione iniziale nel piano Q, quando allora l'angolo al vertice

,

e la si fa poi ruotare attorno all'asse. Si genera una superficie piana se l'angolo al vertice è retto, altrimenti una superficie conica di rivoluzione;

d) la retta BC è sostegno di un tiralinee che può scorrere su di essa finché una delle sue estremità ‒ e sia M ‒ cade nel piano P per tracciare la figura cercata.

La figura DABC è quella del compasso, Q è il piano del compasso.

Tutto dipende dunque dall'angolo β che l'asse del compasso forma con l'asta BC, e dall'angolo α dell'asse con la base del compasso. Il tiralinee ha una lunghezza variabile, e ciò fa sì che la punta resti in contatto con il piano sul quale si vogliono tracciare le sezioni coniche. L'asse resta fisso.

Sia α ottuso, e sia BK la perpendicolare abbassata da B sul piano secante; BK è quindi perpendicolare alla base del compasso. La natura della curva tracciata dipende dall'angolo CBK; si ha

Se quindi:

la sezione è un'ellisse;

,

la sezione è una parabola;

la sezione è un'iperbole.

L'idea di al-Qūhī è che la natura della curva che si vuole tracciare su un piano dipende dalla posizione iniziale del compasso rispetto a questo piano. Questa posizione è caratterizzata dalla lunghezza l dell'asse del compasso, dall'angolo β e dall'angolo α dell'asse con la base del compasso. Si tratta perciò di studiare la corrispondenza tra gli elementi (l, β, α) e gli elementi che caratterizzano la sezione conica: diametro e lato retto per l'ellisse e l'iperbole, lato retto per la parabola.

Al-Qūhī procede allora con lo stabilire le seguenti proposizioni.

a) Se α=π/2 e β=π/2, il tiralinee non incontra il piano P e non traccia nulla.

b) Se α≠π/2 e β=π/2, la retta BC genera un piano che interseca il piano P secondo una retta che sarà tracciata dal tiralinee.

c) Se α=π/2 e β⟨π/2, la curva tracciata è un cerchio di raggio r=AB tg β.

d) Se α=β⟨π/2, la curva tracciata è una parabola di asse AD e vertice D.

e) Se α⟨β⟨π/2, la prima estremità del tiralinee descrive un ramo di iperbole di vertice D, e la seconda l'altro ramo di iperbole di vertice E.

f) Se β⟨ α⟨π/2, il tiralinee traccia un'ellisse.

Per illustrare il procedimento di al-Qūhī prendiamo l'esempio dell'ultimo caso: consideriamo la falda di superficie conica di asse BA e di angolo al vertice β generata dalla semiretta BC. Il piano P interseca tutte le generatrici di questa falda, e l'intersezione è un'ellisse di asse DE. Il punto D è all'estremità del tiralinee quando è nel piano Q con α e β da una stessa parte di AB. Il punto E è l'estremità del tiralinee, sempre nel piano Q, quando α e β sono da una parte e dall'altra di AB. Nella rotazione di BC attorno ad AB il tiralinee traccia l'intera ellisse.

Il compasso perfetto permette così il tracciato continuo, su un piano dato, di una retta, di un cerchio o di una qualunque sezione conica, sia in rapporto a un'asse sia a un diametro. I ragionamenti e le costruzioni indicate da al-Qūhī non fanno mai intervenire i fuochi, ma si basano sulle proprietà stabilite da Apollonio nel Libro I delle Coniche per le sezioni piane di un cono a base circolare e che riguardano un diametro, il lato retto a esso associato e l'angolo formato da questo diametro con la direzione delle rette ordinate.

Il Libro II del trattato è interamente dedicato alla soluzione dei problemi del tracciato continuo delle curve. In ciascuno dei problemi che al-Qūhī affronta, i dati sono gli elementi visti sopra, relativamente alla curva che si vuole tracciare. Egli si chiede quindi come determinare la figura del compasso perfetto, una volta precisata la grandezza dei suoi elementi. Consideriamo brevemente l'esempio della parabola: tracciare una parabola dati il vertice B, il diametro BC, il lato retto D, l'angolo E delle rette ordinate che corrispondono al diametro BC. Si presentano due casi, a seconda che l'angolo in E sia retto o no.

Se E è retto, la retta BC è l'asse della parabola. Al-Qūhī aveva però dimostrato nel Libro I che in questo caso deve essere α=β. Se A è la lunghezza dell'asse del compasso, occorre che

Non è il caso di riprodurre qui il calcolo che conduce al-Qūhī a questa condizione (Rashed 2003a). Ricordiamone soltanto gli inizi. Al-Qūhī comincia con il tracciare un semicerchio di diametro qualunque GH e prende su questo diametro un punto K tale che

Si ha KI perpendicolare a GH. L'angolo KHI è l'angolo cercato per il compasso. Si fa scorrere il tiralinee fino a che l'estremità non incontri la retta del centro. Il compasso è allora rappresentato dal triangolo BLM di asse LM di lunghezza A. Il punto M è il centro, la retta del vertice è LB se l'angolo al vertice e l'angolo al centro sono da una stessa parte dell'asse BM, mentre è LN parallela a BM se questi angoli sono alterni. Si pone la retta del centro BM sulla retta data BC; se si fa ruotare LB attorno a LM il tiralinee retto da LB traccia la parabola cercata.

Se ora l'angolo E non è retto, la retta BC è un diametro qualunque della parabola cercata. Il metodo di al-Qūhī consiste nel definire l'asse di questa parabola, il vertice e il lato retto corrispondente per ricondursi al caso precedente. Riprendiamo il procedimento di al-Qūhī. Per un punto G su uno dei lati dell'angolo dato E, si traccia GH perpendicolare all'al tro lato in H; sia I il punto di mezzo di EH. Si pone

ciò che permette di definire la lunghezza N. Prendiamo ora un punto K sul prolungamento di CB, tale che

KL perpendicolare a BC e KL=N (i triangoli LKB e GHE sono simili, e inoltre LK=N; il triangolo LKB è quindi noto, la lunghezza KB è nota).

Sia O tale che LO è parallela a BC e BO a KL, e M il punto di mezzo di LO. Si definisce una lunghezza S secondo la OB/S=OM/OB. Si sa allora tracciare con il compasso, il cui asse ha lunghezza A, la parabola di diametro MO, vertice M e lato retto S, tale che l'angolo formato dal diametro LO con la retta ordinata sia retto; MO è dunque l'asse della parabola, come al-Qūhī aveva stabilito nel primo caso. Questa parabola passa per B in quanto OB2=S∙OM (ascissa OM, ordina ta OB). È evidente che BC, parallela a MO, è un diametro.

Resta tuttavia da dimostrare che il lato retto associato a BC è D e che l'angolo formato dall'ordinata e dall'asse è l'angolo E; in altri termini, che BL è tangente in B alla parabola. Prendiamo (Mx, My) come sistema di riferimento; la parabola di asse Mx e lato retto S ha allora equazione y2=Sx.

Il vertice M della parabola è il punto di mezzo di OL, e dunque la retta BL è tangente in B alla parabola.

Nel sistema (Bx1, By1), assi obliqui, l'equazione è y12=Tx1, dove T è il lato retto. Le coordinate di M sono x1=LM, y1=LB, da cui LB2=T∙LM. Dimostriamo che T=D. Si ha che KL=N, da cui

si ha:

Al-Qūhī tratta poi in modo analogo il problema di tracciare un'iperbole, noti il diametro trasverso, il lato retto associato, l'angolo formato dal diametro trasverso e la retta ordinata; la lunghezza dell'asse è data. Passa poi al problema di tracciare in un piano dato un'ellisse, noti il diametro, il lato retto associato e l'angolo formato da questo diametro con la propria retta ordinata.

In tutti questi problemi l'autore dimostra che gli angoli α e β sono noti, e pertanto il compasso perfetto è determinato.

Osserviamo che i tre problemi trattati da al-Qūhī corrispondono alle propp. 52-56 del Libro I delle Coni che di Apollonio (Rashed 2002, 2003a). Tutto indica in effetti che al-Qūhī prende, per così dire a titolo di esercizio, i problemi che si trovano alla fine del Libro I delle Coniche, dove Apollonio esamina la costruzione delle sezioni coniche, per mostrare come si possa dare di queste ultime il tracciato continuo mediante il compasso perfetto. Forse egli voleva anche dimostrare che il nuovo strumento e i nuovi metodi erano insieme necessari e validi per la soluzione dei problemi dello stesso Apollonio.

Al-Siǧzī: il compasso perfetto migliorato

Come abbiamo già ricordato al-Siǧzī è un giovane contemporaneo di al-Qūhī, del quale conosceva bene l'opera. Ne conosceva a fondo il trattato sul compasso perfetto: su questo non c'è dubbio. Per convincersene basta leggere attentamente la sua Risāla fī rasm al-quṭū῾ al-maḫrūṭiyya (Epistola sul tracciato delle sezioni coniche) come pure la Risāla fī ῾amal al-birkār al-tāmm, anche se il nome di al-Qūhī non vi compare mai. Ma l'importante non è solo questo. I due titoli sopra citati sono la migliore testimonianza che il problema del tracciato delle curve era diventato sufficientemente centrale perché un solo autore vi dedicasse due trattati. E inoltre: nella Risāla fī rasm al-quṭū῾ al-maḫrūṭiyya, relativamente tarda, vediamo al-Siǧzī occuparsi del tracciato continuo per punti, mediante un modello costruito allo scopo, e mediante il compasso perfetto. Sappiamo d'altra parte che egli aveva dedicato un raffinato studio al tracciato per punti dell'iperbole, e anche un'opera sul compasso perfetto, nella quale trattava ugualmente del tracciato continuo. In quest'ultimo scritto l'autore sembra voler apportare alcune modifiche all'invenzione di al-Qūhī per accrescerne le possibilità: il compasso sarà così in grado di tracciare, oltre alle curve considerate da al-Qūhī, anche sezioni simili. Le modifiche proposte riguardano il modo di articolazione dell'asse e dell'asta del compasso e i dispositivi che permettono di regolare l'angolo che questi formano, e anche il modo di allungare o accorciare l'asse o l'asta sulla quale si trova il tiralinee.

Al-Siǧzī inizia con il presentare un procedimento che ha lo scopo di far variare la lunghezza dell'asse del compasso, senza menzionare la lunghezza della seconda asta, quella sulla quale si trova il tiralinee. È tuttavia sottinteso che la punta del tiralinee debba restare in contatto con il piano sul quale si vuole tracciare la sezione conica. Considera due tubi AN e AS articolati nel punto A, vertice del compasso. Nel tubo AN si trova un'asta AB che è l'asse del compasso, e nel tubo AS l'asta AC che è il sostegno del tiralinee. L'articolazio ne dei due tubi in A permette al tubo AS di ruotare attorno ad A, in modo da poter scegliere l'angolo BAC e permettere ad AS di seguire il tubo AN nel movimento di rotazione attorno all'asse AB. Al-Siǧzī considera poi un arco GE del cerchio di centro A che attraversa due tacche E e G′, rispettivamente sulle pareti di AN e di AS, e che scorre su due scanalature su queste pareti. Serve quindi un dispositivo che permetta di bloccare in ogni momento lo scorrimento e la divaricazione scelta per i due tubi, prima di far ruotare il tubo AS che contiene il tiralinee di un angolo BAC fissato. L'angolo BAC è misurato dal rapporto dell'arco EG ad AE. Fissato l'arco EG, basta far scorrere E e G nelle rispettive tacche per aggiungere la distanza AE e per bloccare la divaricazione.

Al-Siǧzī indica allora tre metodi per regolare la lunghezza dell'asta AB, asse del compasso. Prendiamo per esempio il primo. Si suppone che l'asta AB sia tagliata nel punto P, cioè che sia divisa in due parti: la AP, che si suppone fissa, e la PB, che si può far scorrere nel tubo AN mediante un chiodo con la testa a occhiello, o una leva, posti in P. In questo caso è possibile passare dalla posizione PB alla P1B1. Ciò presuppone che nella parete del tubo AN vi sia una fenditura rettilinea nella quale può scorrere il chiodo con la testa in P. L'asse del compasso raggiunge allora la lunghezza AB1, che corrisponde alla distanza voluta per portare la punta B1 dell'asse nel piano sul quale si vuole tracciare la sezione conica.

Al-Siǧzī presenta quindi un procedimento per far scorrere l'asse che porta il tiralinee nel tubo che costituisce la seconda asta del compasso. Presenta anche un secondo metodo per far variare la lunghezza dell'asse del compasso. Espone infine un terzo procedimento, con la lunghezza dell'asse che resta costante e l'asse del tiralinee sempre supposto mobile. L'idea che risulta da questo scritto di al-Siǧzī si può formulare come segue: qualunque sia il modello di compasso scelto, esso permette il tracciato continuo delle tre sezioni coniche e delle sezioni simili, oltre al cerchio e alla retta.

Per capire quest'ultimo punto ricordiamo che Apollonio nella prop. 11 del Libro VI delle Coniche dimostra che tutte le parabole sono simili: per due parabole di lati retti c e c′ il rapporto di similitudine è c/c′. Nella prop. 12 egli dimostra che la condizione necessaria e sufficiente affinché due ellissi (o due iperboli) di diametro d e d′ e di lati retti c e c′ siano simili è che d/d′=c/c′, ovvero c/d=c′/d.

Consideriamo il solo tracciato della parabola. Supponiamo dato il piano ABC corrispondente alla posizione iniziale del compasso e supponiamo che in questo piano l'asse AB del compasso sia stabilito in posizione e grandezza. Il piano Π sulla quale il compasso può tracciare una sezione co nica è perpendicolare a questo piano e lo interseca secondo una retta XBY sulla quale si trova l'asse della sezione. Poniamo

La questione dunque è la seguente: è possibile tracciare, con queste ipotesi, due sezioni simili?

Come abbiamo appena ricordato, secondo Apollonio tutte le parabole sono simili. Veniamo al piano Π dato e al compasso; un tale compasso permette di tracciare soltanto una parabola. Infatti se Π è dato, β è noto e anche α lo è in quanto α+β=π. Determiniamo il lato retto c di questa parabola di vertice I. Sia M il punto della curva tale che MB sia perpendicolare a IY; si ha allora MB perpendicolare ad AB (in quanto Π è perpendicolare ad ABC) e

,

da cui

[7] MB² = c ∙ BI  e  MB² = l²∙tan2α;

ora BI=l/2 cosα (triangolo isoscele IAB). Ne segue:

Prendendo per l'asse AB una lunghezza l′ (l′ l o l′=l) si traccerà in Π′, definito da

con α′=π−β′, una parabola di lato retto c′=2l′(sen2α′/cosα′), da cui il rapporto di similitudine c′/c. Si possono così tracciare con il compasso due sezioni paraboliche simili in uno stesso piano Π. È l'idea che al-Siǧzī ricorda molto brevemente alla fine del suo scritto.

Così, seguendo al-Qūhī, al-Siǧzī stabilisce in generale che la natura della curva tracciata dipende dalla posizione iniziale del compasso rispetto al piano sul quale la si vuole tracciare.

Le ricerche sul compasso perfetto e il tracciato continuo non finiscono con al-Siǧzī. Come abbiamo detto, altri matematici le proseguiranno per almeno altri due secoli.

Tracciato continuo e classificazione delle curve

Come abbiamo osservato, le ricerche sul tracciato continuo rispondevano tra l'altro alla necessità che avevano i matematici dell'epoca di assicurarsi della continuità delle curve. Il solo mezzo di cui disponevano era quello di introdurre nella geometria il movimento. Ora, queste nuove preoccupazioni indirizzeranno presto questa ricerca verso il problema più importante: la classificazione delle curve in funzione del tipo e del numero di movimenti che intervengono nel loro tracciato. Si tratta di una ricerca fondamentale, l'importanza della quale merita di essere sottolineata.

Al-Qūhī distingue le curve tracciate con il compasso perfetto ‒ retta, cerchio, sezioni coniche ‒ con il nome generico di 'linee qiyāsiyya', che tradurremo con 'linee misurabili'. Ecco quanto scrive all'inizio del libro: "È un trattato sullo strumento che chiamano compasso perfetto, e comprende due libri. Il primo riguarda la dimostrazione del fatto che è possibile tracciare con questo compasso le linee misurabili, qiyāsiyya, cioè le rette, le circonferenze dei cerchi e le circon ferenze delle sezioni coniche ‒ cioè le parabole, le iperboli, le ellissi e le sezioni opposte" (Rashed 2003a). Questo termine linee misurabili sarà utilizzato lungo tutta la tradizione: lo ritroviamo in al-Siǧzī, Hibat Allāh al-Baġdādī, Ibn al-Ḥusayn, ecc. Ma nella traduzione francese di Franz Woepcke esso viene reso con 'linee regolari', oscurando in questo modo un fatto importante.

L'aggettivo plurale qiyāsiyya deriva dal verbo qāsa, yaqīsu, o da qāsa, yaqūsu, che esprimono entrambi l'idea di misura, donde la traduzione letterale linee misurabili. Lo stesso termine qiyāsī (al singolare) ha anche un senso figurato: si dice per esempio di una donna che cammina con un'andatura regolare, ed è questo senso figurato che Woepcke accoglie quando parla di linee regolari. Una traduzione niente affatto soddisfacente, non soltanto perché privilegia arbitrariamente il senso figurato, ma in ragione della sua ambiguità e imprecisione. Se si vuole parlare di curva regolare, con il significato che ne viene dato a partire dal XIX sec., bisogna allora escludere la retta. Invece per al-Qūhī anche la retta fa parte di queste linee qiyāsiyya.

Cosa intende allora al-Qūhī quando parla di linee misurabili? Nella terminologia della geometria dell'epoca sono linee, cioè grandezze, che rispondono alla teoria delle proporzioni. È questo il significato che intende al-Qūhī. Si tratta dunque di linee generate da un unico movimento continuo ‒ quello dell'asta del compasso perfetto ‒ e alle quali si può applicare la teoria delle proporzioni. È il caso della retta e del cerchio, ma anche delle tre sezioni coniche caratterizzate dai symptómata o dalle proprietà del fuoco e della direttrice.

Con al-Qūhī si viene così a stabilire una classificazione delle curve: le curve misurabili e le altre; ma si supera anche una distinzione, radicata nella tradizione, tra la retta da una parte e le curve (tra cui il cerchio) dall'altra.

Al-Siǧzī non soltanto fa propri questi risultati di al-Qūhī ma li precisa. In un libro dal titolo Kitāb al-Madḫal ilā ῾ilm al-handasa (Libro d'introduzione alla scienza della geometria) procede a diverse classificazioni. Quando arriva a parlare delle linee ne distingue tre specie: misurabili (retta, cerchio e sezioni coniche), non misurabili ma dotate di ordine (niẓām) e di regolarità (tartīb), e infine non misurabili, senza ordine e regolarità. Le prime sono generate con un solo movimento continuo e sono 'geometriche', cioè utilizzate in geometria. Le seconde sono generate con due movimenti continui: non sono 'geometriche', bensì 'meccaniche'. Le ultime, pure generate con due movimenti continui, non sono nemmeno meccaniche. L'esempio che egli fornisce di curva meccanica è l'elica cilindrica. Si tratta in effetti di una curva sghemba, generata da un movimento di rotazione uniforme attorno a un asse e da una traslazione uniforme parallela all'asse. Ecco cosa scrive: "Quanto alla curva, l'elica cilindrica (al-ḫaṭṭ al-lawlabī), utilizzata in meccanica (al-ḥiyal) e non in geometria in quanto non misurabile (ġayr qiyāsī) ma dotata di ordine e di regolarità, è generata dal movimento di un punto secondo una retta e un cerchio, di solito con il cilindro" (ms. Dublino, Chester Beatty 3652, f. 4r). E prosegue:

Eccone la figura: sia dato il cilindro ABCD le cui due basi sono AB e CD. Se immaginiamo che il punto A si muova con moto uniforme secondo la retta AC e che il cilindro ruoti attorno ai due centri delle basi con moto uniforme, si viene a generare la linea AEGHID che è un'elica cilindrica. Quanto alle linee che non hanno ordine, esse non hanno allora né limite [ḥadd, che si traduce anche con 'definizione'] né estremità, e non vengono utilizzate in alcuna delle arti; è questo il motivo per cui non vengono descritte né definite. (ibidem)

Al-Siǧzī traccia l'elica cilindrica, ma non fornisce alcun esempio di curva non misurabile senza ordine e regolarità. Pensava forse a curve come la quadratrice o la spirale.

Non c'è quindi ombra di dubbio sul senso della distinzione tra curve misurabili e non misurabili. Un'ulteriore dimostrazione del significato di questi termini si trova nell'uso che ne fa al-Siǧzī quando definisce gli angoli: gli angoli non misurabili sono quelli curvilinei e l'angolo di contingenza, mentre gli angoli misurabili sono quelli che si possono studiare mediante la teoria delle proporzioni (f. 68r).

Questa ricerca fondamentale sulla classificazione delle curve tramite la nozione di movimento e di numero di movimenti, e la divisione tra curve geometriche e curve meccaniche a seconda che sia possibile o meno applicare la teoria delle proporzioni, è di importanza capitale nella storia della geometria, in particolare ‒ molto più tardi ‒ della geometria algebrica. Si tratta ora di sapere quale sia stato il destino di questo capitolo nella matematica posteriore ai secc. X e XI, capitolo di cui abbiamo qui soltanto delineato la storia.

Bibliografia

Rashed 1987: Rashed, Roshdi, Al-Sijzī et Maïmonide: commentaire mathématique et philosophique de la proposition II-14 des Coniques d'Apollonius, "Archives internationales d'histoire des sciences", 119, 1987, 37, pp. 263-296 (trad. ingl.: Conceivability, imaginability and probability in demonstrative reasoning: al-Sijzī and Maimonides on II.14 of Apollonius' conics sections, "Fundamenta scientiae", 8, 1987, 3-4, pp. 241-256).

‒ 1990: Rashed, Roshdi, A pioneer in anaclastics. Ibn Sahl on burning mirrors and lenses, "Isis", 81, 1990, pp. 464-491.

‒ 1993: Rashed, Roshdi, Géométrie et dioptrique au X^e siècle: Ibn Sahl, al-Qūhī et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.

‒ 1997: Œuvres philosophiques et scientifiques d'al-Kindī, Leiden, E.J. Brill, 1997-1998, 4 v.; v. I: L'optique et la catoptrique, par Roshdi Rashed, 1997.

‒ 2000a: Rashed, Roshdi, Les catopriciens grecs, textes établis, traduits et commentés par Roshdi Rashed, Paris, Les Belles Lettres, 2000-; v. I: Les miroirs ardents, 2000.

‒ 2000b: Rashed, Roshdi, Math. inf. III.

‒ 2000c: Rashed, Roshdi - Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, Leiden, E.J. Brill, 2000.

‒ 2002: Rashed, Roshdi, Math. inf. IV.

‒ 2003a: Rashed, Roshdi, Geometry and geometrical optics in the 10th-11th century: Ibn Sahl, al-Qūhī and Ibn al-Haytham, London, al-Furqān Islamic Heritage Foundation, 2003.

‒ 2003b: Rashed, Roshdi, Al-Qūhī et al-Sijzī: sur le compas parfait et le tracé continu des sections coniques, "Arabic sciences and philosophy", 13, 2003, 1, pp. 9-45.

Tannery 1884: Tannery, Paul, Eutocius et ses contemporains, "Bulletin des sciences mathématiques", s. II, 8, 1884, pp. 315-329 (rist. in: "Mémoires scientifiques", t. II, pp. 118-136).

Woepcke 1874: Woepcke, Franz, Trois traités arabes sur le compas parfait, "Notices et extraits des manuscrits de la Bibliothèque Impériale et autres bibliothèques", 22, 1874, pp. 1-175.