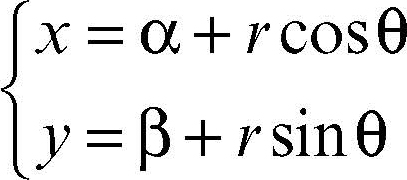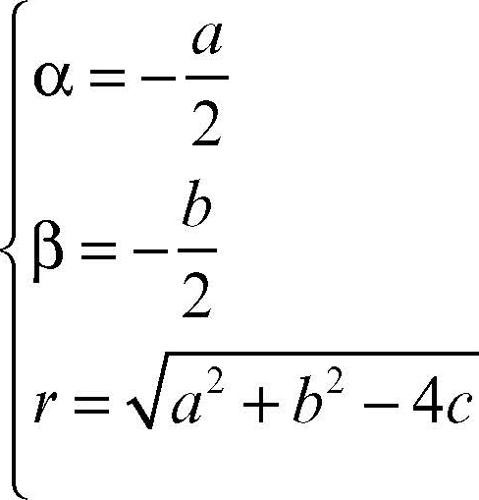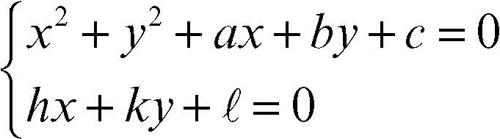circonferenza

circonferenza

circonferenza luogo dei punti del piano aventi la stessa distanza, detta raggio (r), da un punto fisso O, detto centro. La superficie piana racchiusa da una circonferenza è detta cerchio. Una circonferenza è simmetrica rispetto al proprio centro e rispetto a ogni retta passante per esso. Indicando con r la misura del raggio e con l_c la lunghezza della circonferenza c, si ha: l_c = 2πr. Una circonferenza è univocamente individuata assegnandone il centro e il raggio oppure assegnando tre punti non allineati. Due punti distinti su una circonferenza individuano su di essa due parti, ciascuna delle quali è detta arco di circonferenza. La lunghezza di un arco dipende dalla misura del corrispondente angolo al centro ed equivale a 2πrα/360°, essendo r il raggio della circonferenza. Una corda di una circonferenza è un qualsiasi segmento avente gli estremi su di essa. Se la corda passa per il centro è detta diametro e ha la massima lunghezza 2r. Tra le proprietà delle corde si ricordano le seguenti:

• due corde sono uguali se e solo se hanno la stessa distanza dal centro;

• l’asse di una qualsiasi corda passa per il centro.

Quest’ultima proprietà permette di stabilire che per tre punti non allineati passa una e una sola circonferenza e ne permette la costruzione. Dati infatti tre punti non allineati A, B, C, è sufficiente tracciare due dei tre assi del triangolo ABC. L’intersezione degli assi (circocentro) è il centro della circonferenza per i tre punti dati.

Tra le proprietà geometriche della circonferenza, una delle più notevoli è la cosiddetta proprietà isoperimetrica: fra tutte le linee chiuse di data lunghezza la circonferenza è quella che racchiude area massima (o, in altri termini, tra le linee che racchiudono un’area data la circonferenza è quella di lunghezza minima). La circonferenza è una particolare conica: è infatti ottenibile come sezione della superficie di un cono circolare retto con un piano perpendicolare al suo asse.

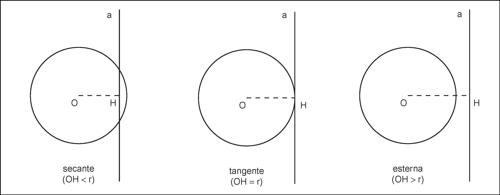
Una circonferenza γ e una retta a, in uno stesso piano, possono intersecarsi o meno a seconda della loro posizione reciproca; si hanno al riguardo i seguenti casi:

• se la distanza di a dal centro di γ è minore del raggio, si hanno due punti di intersezione distinti e la retta a è detta retta secante alla circonferenza;

• se la distanza di a dal centro di γ è uguale al raggio, si hanno due punti di intersezione coincidenti e la retta a è detta retta tangente alla circonferenza;

• se la distanza di a dal centro di γ è maggiore del raggio, non ci sono punti di intersezione e la retta è detta retta esterna alla circonferenza.

Fissato nel piano un riferimento cartesiano Oxy, le equazioni parametriche di una circonferenza di centro C(α, β) e raggio r sono:

Per eliminazione del parametro θ si ottiene l’equazione cartesiana (x − α)² + (y − β)² = r ², che può essere riscritta nella forma x ² + y ² + ax + by + c = 0, avendo posto a = −2α, b = −2β, c = α² + β² − r ². Ricavando α, β, r in funzione di a, b, c si ha:

Poiché r ≥ 0, deve risultare a² + b² − 4c ≥ 0. Tale disuguaglianza è detta condizione di realtà del raggio. L’equazione di una circonferenza in coordinate polari, assegnato il centro C(ρ₀, θ₀) e il raggio r, è ρ² + 2ρ₀ρcos(θ – θ₀) + ρ₀² = r ².

Per determinare analiticamente l’equazione di una circonferenza passante per tre punti assegnati si risolve il sistema formato dalle tre condizioni di passaggio, ottenute imponendo che l’equazione della circonferenza sia soddisfatta dalle coordinate dei tre dati punti. Tale sistema, qualunque sia la forma scelta per l’equazione della circonferenza, è un sistema lineare di tre equazioni in tre incognite e, se i tre punti dati non sono allineati, ammette una e una sola soluzione.

Per determinare analiticamente le intersezioni tra una retta e una circonferenza si risolve il sistema formato dalle equazioni delle due curve

detto sistema retta-circonferenza, che, risultando un sistema di secondo grado, può avere due soluzioni reali distinte (retta secante), due soluzioni reali coincidenti (retta tangente), nessuna soluzione reale (retta esterna).

Per determinare l’equazione della tangente a una circonferenza di equazione x ² + y ² + ax + by + c = 0, in un suo punto P₀(x₀, y₀), si può utilizzare la cosiddetta regola di sdoppiamento:

(retta tangente a una conica). Una circonferenza qualunque interseca la retta impropria del piano in due punti immaginari coniugati, detti punti ciclici (tale proprietà è caratteristica: ogni conica passante per i punti ciclici è una circonferenza); ne consegue che il fascio di coniche individuato da due circonferenze è interamente formato da circonferenze (è un fascio di circonferenze). Facendo variare, in tutto lo spazio, il piano della circonferenza, i punti ciclici descrivono una conica immaginaria detta circonferenza assoluta o cerchio assoluto.

Tra i problemi classici legati alla circonferenza vanno ricordati la → ciclotomia, cioè la divisione della circonferenza in parti uguali che si identifica con il problema della costruzione dei poligoni regolari di n lati inscritti nella circonferenza, e la → rettificazione, cioè la possibilità di costruire, a partire dal diametro (o dal raggio), un segmento avente lunghezza uguale a quella della circonferenza; il problema è oggi risolto con la esatta conoscenza della natura del rapporto π esistente tra la lunghezza della circonferenza e il suo diametro 2r; tale rapporto è un numero irrazionale e trascendente, da cui l’impossibilità di risolvere il problema della rettificazione (e della conseguente quadratura del cerchio) con i mezzi elementari, quali la riga e il compasso.