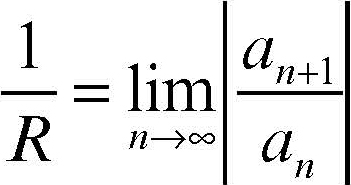convergenza, cerchio di
convergenza, cerchio di
convergenza, cerchio di per una serie di potenze nel campo complesso
cerchio, con centro nell’origine, avente raggio R (detto raggio di convergenza) che può assumere qualsiasi valore finito positivo o +∞. Nei punti interni a tale cerchio, quando cioè |z| < R, la serie converge assolutamente e totalmente, se invece |z| > R, la serie non converge. Nei punti corrispondenti alla cosiddetta circonferenza di convergenza |z| = R, la serie può convergere o non convergere, a seconda dei casi.
Per esempio, ∀p la serie
ha raggio di convergenza 1, ma tale serie sulla circonferenza |z| = 1:
• per p = 0 non converge in alcun punto;
• per p = 1 converge in tutti i punti eccetto z = 1;
• per p = 2 converge ovunque.
Sulla circonferenza di convergenza esiste comunque almeno un punto singolare per la funzione analitica ƒ(z) somma della serie di potenze; il raggio di convergenza può essere interpretato geometricamente come la distanza dall’origine del più vicino dei punti singolari di ƒ(z). Negli esempi precedenti il punto z = 1 è singolare, in quanto la somma della serie data è rispettivamente:
per p = 0;
• −log(1 − z) per p = 1;
• una primitiva di (−1/z) log(1 − z) per p = 2.
Se R = 0 la serie converge solo in z = 0 (dove vale per convenzione a0); se R = ∞ la convergenza sussiste in tutto il piano complesso. La convergenza è sempre assoluta per |z| < R, e totale in ogni cerchio |z| ≤ r, con r < R. Il valore del raggio di convergenza è dato da:
o da
(con le convenzioni 1/0 = ∞, 1/∞ = 0), quando uno di tali limiti esiste e, più in generale, dalla formula di → Cauchy-Hadamard. Per esempio, la serie esponenziale
ha raggio di convergenza ∞, la serie
ha raggio di convergenza 0, la serie
ha raggio di convergenza R. Nel caso di una serie del tipo
il cerchio di convergenza ha centro in z0 e tutto il resto rimane invariato a meno di una traslazione di vettore z0.