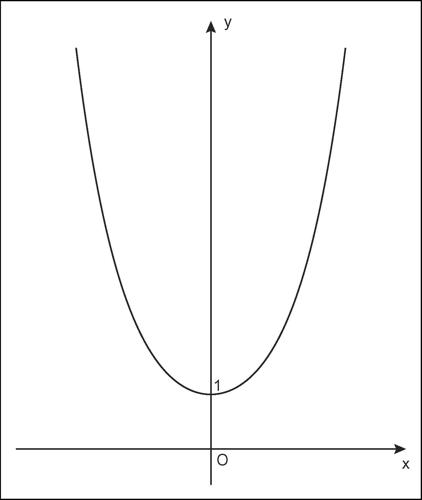
catenaria

Enciclopedia della Matematica (2013)

catenaria


catenaria curva piana il cui andamento assume la configurazione di una fune (omogenea, perfettamente flessibile e non estensibile), soggetta soltanto al proprio peso e i cui due estremi siano vincolati a due punti fissi. La catenaria è una curva trascendente, la cui equazione si esprime mediante la funzione coseno iperbolico:

formula

Il grafico di una catenaria può confondersi con quello di una parabola, ma non è una parabola, anche se nel vertice sono praticamente coincidenti. La catenaria ha la proprietà di avere in ogni suo punto una distribuzione uniforme del suo peso totale. Essa è il luogo geometrico dei punti nei quali le tensioni orizzontali di un cavo si compensano; in questo modo, il cavo non ha tensioni laterali e non si sposta verso i lati. Per questa ragione alcune strutture, come per esempio i cavi della linea elettrica o quelli delle funivie, descrivono curve che non si discostano sensibilmente da una catenaria. Nelle ferrovie elettriche con alimentazione aerea, si usa la sospensione a catenaria della linea di contatto elettrico, per mantenere il filo conduttore a un’altezza uniforme rispetto al terreno.

CATENARIA

Vedi anche
evoluta fig.In geometria si chiama e. (o sviluppata) di una curva piana C la curva Γ, luogo geometrico dei centri di curvatura dei punti di C; si dice allora che la curva C è una evolvente (o sviluppante) di Γ. Essa può anche definirsi come inviluppo delle normali a C; se infatti (come in fig.) P è un punto ... trattrice fig.trattrice (o t. della retta) In matematica, la curva piana caratterizzata dal fatto che il segmento di tangente compreso tra il punto di contatto M e una retta fissa è costante (v. fig.). Se k è la misura del segmento e l’asse x è la retta data, si hanno le equazioni parametriche x=k logtg(ϕ/2)+k ... statica Parte della meccanica che studia l’equilibrio dei corpi sotto l’azione di determinate sollecitazioni; a seconda del sistema mediante il quale i corpi sono rappresentati si distinguono una s. del punto, una s. dei sistemi rigidi o stereostatica, una s. dei sistemi continui ecc. In particolare, nella scienza ... Gottfried Wilhelm von Leibniz Filosofo e scienziato (Lipsia 1646 - Hannover 1716). Dopo aver studiato filosofia a Lipsia, matematica a Jena e diritto a Altdorf, entrato in rapporto con i Rosacroce conobbe Johann Christian barone di Boineburg: gli incarichi che ebbe da questo gli permisero di entrare in contatto, a Parigi, con le ...
Tag
Altri risultati per catenaria
  • catenaria
    Enciclopedia on line
    In geometria, curva piana trascendente caratterizzata dalla seguente proprietà differenziale: fissato un punto V della curva (v. fig.), la lunghezza di un arco, avente un estremo in V e l’altro estremo in un punto A variabile su di essa, è proporzionale alla tangente trigonometrica dell’angolo ϕ formato ...
  • catenaria
    Dizionario delle Scienze Fisiche (1996)
    catenària [Der. di catena] [ALG] Curva piana non algebrica, caratterizzata dalla seguente proprietà differenziale: fissato (v. fig.) un punto V della curva, la lunghezza di un arco avente un estremo in V e l'altro estremo in un punto A variabile su di essa, è proporzionale, per una costante di proporzionalità ...
  • CATENARIA
    Enciclopedia Italiana (1931)
    La catenaria ordinaria è la curva piana secondo cui si dispone una fune o catena omogenea pesante, quando se ne fissino gli estremi: avendo essa l'aspetto generale di una parabola, Galileo aveva ritenuto fosse appunto una linea di tale specie; l'errore venne rilevato e corretto da C. Huygens. Nel piano ...
Vocabolario
catenària
catenaria catenària agg. e s. f. [der. di catena]. – 1. a. In geometria, curva piana non algebrica, luogo del fuoco di una parabola che rotola senza strisciare sopra una retta fissa. b. In meccanica, c. omogenea, configurazione di equilibrio...
catenòide
catenoide catenòide s. f. [comp. di catena e -oide]. – In geometria, superficie che si ottiene facendo ruotare una catenaria intorno alla sua direttrice.