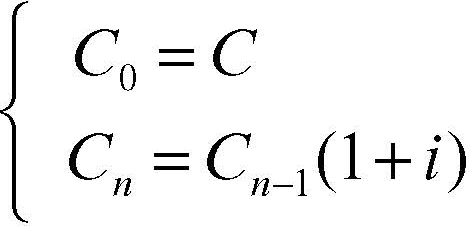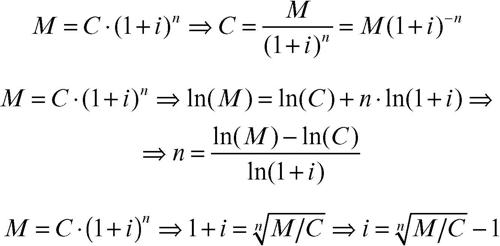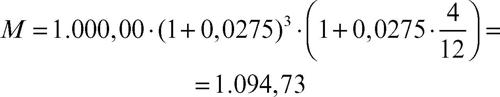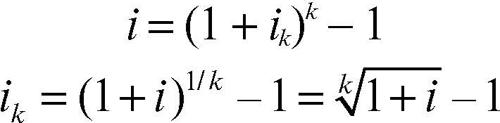capitalizzazione composta

capitalizzazione composta

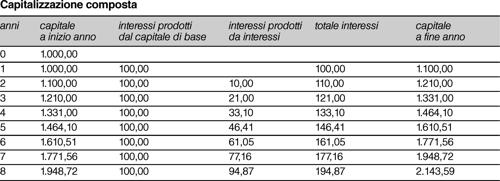
capitalizzazione composta operazione finanziaria nella quale gli interessi relativi a ogni periodo di capitalizzazione non vengono scorporati dal capitale, ma producono essi stessi ulteriori interessi. Per ogni periodo unitario di tempo, in regime di capitalizzazione composta, gli interessi sono proporzionali al capitale iniziale, cioè al capitale esistente all’inizio di ogni periodo (non per l’intera durata del prestito o di un deposito bancario). Per esempio, un capitale iniziale di 1.000,00 euro, investito al tasso del 10% annuo (valore usato per semplicità di calcolo), dopo un anno produce 100,00 euro di interessi, che, durante il secondo anno, a loro volta produrranno interessi (ulteriori 10,00 euro in aggiunta ai 100,00 prodotti dal capitale iniziale di 1.000,00 euro). Nella tabella è riportato un esempio di calcolo di interessi anno per anno.

Nella colonna «interessi prodotti da interessi» è stato calcolato il 10% della differenza tra capitale a fine anno e capitale iniziale. In base al principio sopra enunciato, il valore del capitale dopo n periodi di tempo può essere sinteticamente descritto mediante una funzione ricorsiva:

Le variabili C e i rappresentano rispettivamente il capitale iniziale e il tasso di interesse. Sviluppando la precedente legge ricorsiva, si perviene alla legge della capitalizzazione composta, detta anche legge esponenziale di capitalizzazione, che consente il calcolo diretto del montante, cioè del capitale finale dopo un determinato periodo di tempo, fissato un tasso di interesse. Indicando con M il montante, con i il tasso di interesse e con C il capitale iniziale, si ha: M = C · (1 + i)ⁿ. Il fattore (1 + i) è detto fattore di capitalizzazione composta ed è a volte indicato con la lettera u. In base a questa convenzione, la legge di capitalizzazione composta può anche essere indicata nel seguente modo: M = C · u ⁿ.

Risolvendo la legge esponenziale della capitalizzazione rispetto alle diverse variabili che in essa compaiono, si ottengono le formule per il calcolo del capitale iniziale C, del tempo n o del tasso di interesse i:

Le moderne calcolatrici scientifiche hanno reso praticamente inutile l’uso delle tavole finanziarie, cioè di tavole nelle quali sono tabulati i valori relativi al montante di una unità di capitale per determinati valori di tassi di interesse. Quando il periodo di tempo rispetto al quale calcolare il valore del montante non è un numero naturale, si possono utilizzare due diversi modelli di calcolo.

Modello della convenzione esponenziale

L’intero periodo di tempo viene considerato come un unico valore e si applica direttamente la legge esponenziale: M = C · (1 + i)^t, con t ∈ R. Per esempio, il montante dopo 3 anni e 4 mesi di un capitale iniziale di 1.000,00 euro, al tasso annuo del 2,75%, si ottiene nel modo seguente: M = 1.000,00 · (1 + 0,0275)^{3 + 4/12} = 1.094,64.

Modello della convenzione lineare

Il periodo complessivo di tempo viene scomposto in multipli e frazioni dell’unità: per la parte intera si applica il modello esponenziale e per la parte frazionaria si applica il modello della → capitalizzazione semplice. Indicando con n il numero intero di unità di tempo e con h/k la parte frazionaria residua, si ha:

Per esempio, con gli stessi precedenti dati si ha:

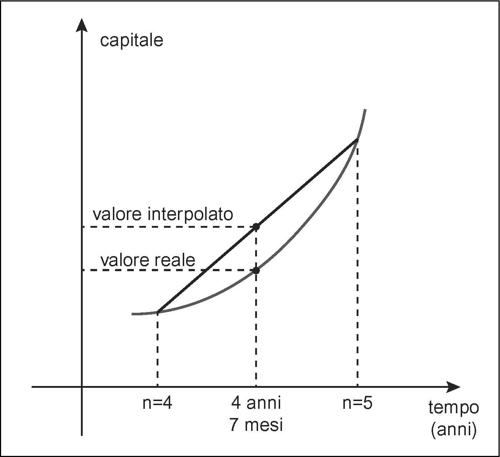
In questo caso si dice anche che si opera in un regime di capitalizzazione mista poiché il calcolo viene appunto effettuato in parte con il modello della capitalizzazione composta (periodi interi di tempo) e in parte con il modello della capitalizzazione semplice (parte frazionaria dell’unità di tempo). In pratica, l’utilizzo della convenzione lineare equivale a effettuare una interpolazione lineare tra due punti. L’approssimazione del valore del montante che così si determina è per eccesso.

Nei processi di capitalizzazione il tasso di interesse può essere riferito a unità diverse da quelle in cui è misurato il tempo; per esempio, con un tasso annuale, la capitalizzazione può avvenire per trimestri. In base al principio di equivalenza finanziaria, se si indica con i_k il tasso periodale di interesse, cioè il tasso di interesse riferito a un k-esimo di unità di tempo, per un capitale unitario, deve valere la seguente uguaglianza:

In casi come questi si parla di capitalizzazione frazionata. Risolvendo la precedente equazione rispetto alla variabile i oppure alla variabile i_k si ottengono le relazioni per calcolare il tasso annuale equivalente a un determinato tasso periodale di periodo k e viceversa: