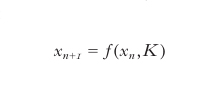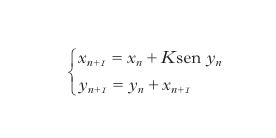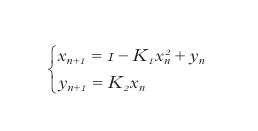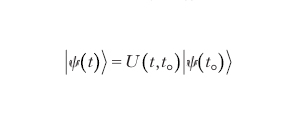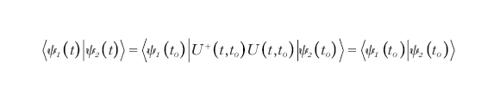Caos e complessità
Caos e complessità
Il caos, nel linguaggio della fisica e della matematica moderna, identifica la situazione di impossibilità di stimare a priori con certezza il valore futuro delle grandezze che caratterizzano un sistema fisico in evoluzione. L'accuratezza finita della conoscenza dello stato iniziale del sistema determina l'impredicibilità, ossia l'impossibilità di determinare, dopo un tempo finito, lo stato futuro di esso. Sebbene l'evoluzione dinamica sembri assumere un aspetto casuale, l'esistenza di leggi deterministiche non lineari alla base di questi sistemi, ne consentono lo studio e la classificazione tramite l'apparato matematico. Il caos si presenta essenzialmente sotto due forme. Nei sistemi conservativi, di cui quelli hamiltoniani sono un importante sottoinsieme, il volume nello spazio delle fasi si conserva nel corso dell'evoluzione temporale del sistema. Nei sistemi dissipativi, il volume decresce a causa di processi irreversibili, come per es. la viscosità o la conduzione termica. Per ambedue le classi di sistemi il caos è il risultato di successivi allungamenti e piegamenti degli elementi di volume dello spazio delle fasi. Il Sistema solare ha un comportamento caotico ed è un esempio di caos conservativo, più precisamente hamiltoniano, la turbolenza di un fluido viscoso come l'atmosfera, anche se infinitesima, costituisce un esempio di caos dissipativo.
L'insieme delle traiettorie di un sistema dinamico caotico evolve verso una struttura frattale chiamata attrattore. Lo studio dell'attrattore consente una quantificazione dell'orizzonte di predicibilità del sistema, ossia del limite spazio-temporale di predicibilità del sistema. L'orbita di un sistema caotico dissipativo converge a un sottoinsieme dello spazio delle fasi di volume nullo. A causa dei successivi piegamenti e allungamenti gli attrattori di un sistema caotico dissipativo hanno una struttura infinito-foliata che è all'origine della denominazione di attrattore strano data a questi oggetti.
Nel caso hamiltoniano l'azione del caos risulta in una decomposizione dell'intero spazio delle fasi in una struttura simile all'insieme di Cantor, con zone di regolarità e stocasticità dei moti. Una applicazione del caos hamiltoniano è legata al problema della formazione e della configurazione orbitale dei sistemi solari. La scoperta di sistemi planetari extrasolari, in cui le distanze, in unità astronomiche, di pianeti fluidi giganti rispetto alla stella risultano minori rispetto a quelle del nostro sistema, dove Giove e Saturno sono posizionati nella parte periferica in relazione ai pianeti terrestri (Mercurio, Venere, Terra e Marte), ha consentito la realizzazione di simulazioni matematiche nelle quali la caoticità gioca un ruolo importante nei meccanismi di migrazione planetaria e di eccentricità delle orbite.
Il concetto di caos trova vaste applicazioni in campo scientifico, soprattutto nello studio dei sistemi complessi. Ciò che accomuna un sistema complesso a un sistema caotico è la non linearità. In questa visione di complessità i sistemi caotici sono considerati un sottoinsieme dei sistemi complessi: la complessità si manifesta infatti sulla soglia della caoticità.
L'ipotesi che sistemi deterministici possano sviluppare comportamenti impredicibili fu teorizzata per la prima volta dal matematico francese H. Poincarè già nello studio del problema dei tre corpi (1890). Aspetti teorici furono inoltre trattati da J. Hadamard (1898) nell'analisi del comportamento dei flussi geodetici su varietà compatte a curvatura negativa: per es., una sfera con due manici. L'avvento della teoria della relatività e della meccanica quantistica agli inizi del secolo scorso relegarono tale campo a un ambito ristretto della meccanica classica, noto come teoria dei sistemi dinamici. Le basi di questa disciplina furono maggiormente sviluppate dalla scuola sovietica di A.N. Kolmogorov, di cui si ricorda il teorema KAM (dalle iniziali di Kolmogorov, Arnol'd, Moser) e la teoria iperbolica, insieme a quella americana con i lavori di G. Birkhoff sulla teoria ergodica (1932). L'elevato grado di astrattezza della teoria dei sistemi dinamici, culla tra l'altro della teoria della complessità, contribuì inoltre all'isolamento di tali idee nell'ambito della fisica teorica e nel resto della ricerca scientifica.
L'importanza della teoria del caos fu pienamente riscoperta e apprezzata agli inizi degli anni Settanta, grazie ai precedenti lavori di E. Lorenz (1963), già allievo di Birkhoff, su un sistema dinamico simulante la termoconvezione. D. Ruelle e F. Takens (1971) contribuirono a esportare il concetto di caos nel campo della turbolenza e quindi della fisica teorica. Il premio Nobel per la chmica I. Prigogine (1977) estese i concetti derivanti dal limite di predicibilità allo studio dei sistemi in non equilibrio, gettando le fondamenta della teoria dei sistemi complessi e dei fenomeni di autoorganizzazione.
In campo puramente matematico, l'ausilio del computer ha dato inoltre spunto alla nascita di ciò che D. Hofstadter ha definito matematica sperimentale, ovvero la simulazione numerica di sistemi dinamici basati su semplici leggi di reiterazione. Un risultato interessante in questo campo è stata la scoperta del numero universale di Feigenbaum (1975), costante numerica supposta trascendentale al pari del numero π e del numero e di Nepero. In tale ambito è stata inoltre sviluppata la teoria dei frattali, oggetti geometrici che godono della proprietà di autosimilarità a ogni scala e di dimensione geometrica non intera, a opera di B. Mandelbrot (1975). Molti dei risultati raggiunti da Mandelbrot si basano sull'utilizzo del calcolatore nello studio delle reiterazioni nel campo dei numeri complessi, avviato negli anni Venti da parte dei matematici francesi G. Julia e P. Fatou. Gli studi svolti nell'ultima parte del secolo scorso hanno mostrato una vasta applicabilità dei concetti derivanti da tali teorie a diverse discipline, dall'economia alla chimica, dall'ingegneria alla biologia, segnando inoltre risvolti interessanti anche in campo artistico (per es., la Computer Art) e filosofico, ed elevando in tal modo il caos al rango di scienza multidisciplinare. Un sistema deterministico è rappresentato da uno stato iniziale e da un insieme di leggi matematiche, spesso non lineari, che ne determinano l'evoluzione temporale, denominata traiettoria, nell'insieme delle configurazioni possibili, detto spazio delle fasi. Tali leggi matematiche sono dipendenti dalla variabile temporale e dalla dimensionalità dello spazio delle fasi. Nel caso di sistemi discreti nel tempo esse sono rappresentate da equazioni algebriche del tipo
dette mappe iterative, dove f è una generica funzione, K un parametro e n l'indice temporale. Per sistemi a variabile temporale continua, la dinamica viene descritta da equazioni differenziali ordinarie nel caso di spazio delle fasi finito, o alle derivate parziali nel caso opposto.
Lo studio dei sistemi caotici a dimensione infinita, detto anche caos spazio-temporale, è un campo di ricerca molto attivo; un esempio è il problema della turbolenza in fluidodinamica.
Un aspetto interessante dei sistemi a dimensione infinita è che molte equazioni non lineari sono state risolte analiticamente grazie alle notevoli proprietà di simmetria di queste ultime. Tali soluzioni sono descritte da oggetti matematici come i solitoni in idrodinamica, onde solitarie con proprietà dinamiche corpuscolari, e da corrispettive generalizzazioni relativistiche quali il concetto di instantone e monopolo nelle teorie di gauge: la relazione tra caos spazio-temporale e rottura di simmetria è argomento di particolare interesse in fisica teorica, in quanto le teorie di campo che descrivono le forze fondamentali, a esclusione dell'elettromagnetismo, sono non lineari. In genere, la difficoltà di tali studi è dovuta principalmente alle strutture metriche degli spazi a dimensione infinita e molti risultati sono riferiti ai sistemi originati da troncamenti in spazi delle fasi finiti. Lo studio delle mappe è a sua volta una potente semplificazione per ricercare il comportamento caotico in tali sistemi finiti.
Il numero K, detto parametro di controllo, è tale che la sua variabilità definisce i confini tra moti regolari e andamenti caotici. Generalmente esso può essere associabile a un elemento forzante esterno al sistema.
Per i sistemi conservativi vale il teorema di ricorrenza di Poincarè, che implica una probabilità non nulla per una traiettoria di passare in un intorno infinitesimamente prossimo a un suo precedente passaggio. È interessante notare che tutte le leggi della fisica, dal moto newtoniano di una particella alle teorie quantistiche di campo, sono riconducibili a sistemi hamiltoniani che notoriamente conservano l'energia. Un sistema hamiltoniano è detto integrabile se è possibile risolverne analiticamente le equazioni del moto. Le traiettorie di un sistema integrabile sono rappresentate da eliche, chiuse o aperte, confinate su uno spazio periodico, definito in una geometria toroidale.
In un sistema energeticamente confinato, proprietà consueta nella rappresentazione matematica dei fenomeni naturali, la variazione della distanza tra due traiettorie, inizialmente vicine, caratterizza durante il loro moto il comportamento dinamico del sistema stesso. La misura della separazione delle orbite è definita esponente di Lyapunov.
Uno dei paradigmi della moderna teoria dei sistemi caotici finiti è che l'instabilità locale delle traiettorie influenzi la dinamica globale del sistema generandone un comportamento stocastico. Tale comportamento, definito iperbolicità, deriva dalla non linearità delle leggi che regolano la dinamica del sistema, che determina una marcata dipendenza del moto dalle condizioni iniziali. Un punto è definito iperbolico se il suo intorno è simile alla superficie di una sella, in cui esiste una decomposizione di aree di attrazione e repulsione rispetto al centro. L'iperbolicità è detta uniforme se vale in ogni punto dello spazio generato dalle traiettorie; altrimenti si definisce non uniforme. Il grado di iperbolicità genera quindi una gerarchia dei sistemi caotici. Sistemi dissipativi iperbolici danno luogo al caos dissipativo.
Un esempio di caos hamiltoniano, dovuto al matematico russo B. Chirikov (1979), è la mappa standard
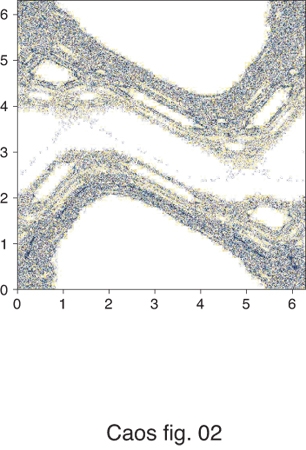
dove xn e yn sono le grandezze che definiscono il sistema all'istante n-esimo; esso ha applicazioni in vari campi della fisica, quali la teoria dei plasma, la fisica degli acceleratori di particelle e la meccanica celeste. Lo spazio delle fasi associato a questo sistema dinamico deterministico è il toro [0,2π]×[0,2π]. Per qualsiasi valore del parametro di controllo K ogni porzione di area del toro viene conservata; inoltre, per K=0 la coordinata x è un'invariante del moto, la traiettoria nello spazio delle fasi si riduce a un'elica chiusa che avvolge il toro e il sistema è integrabile. Al variare del parametro di controllo, la traiettoria ricopre in modo stocastico e denso una frazione dell'intera area, delimitata da isole precluse alla dinamica del sistema (fig. 1). Tale comportamento, riscontrabile per un qualunque insieme di condizioni iniziali, è dovuto alle proprietà di iperbolicità e di ricorrenza di Poincarè, e mostra una struttura di autosimilarità a tutte le scale (fig. 2). L'intero spazio delle fasi assume quindi una struttura simile a un frattale, con le proprietà di un insieme di Cantor, ma di dimensione di Hausdorff intera: tecnicamente esso è definito fat fractal. Aree di completa caoticità, o mare stocastico, si alternano a isole di moti regolari. L'aspetto peculiare della convivenza tra regimi regolari e comportamenti stocastici nel caos hamiltoniano ha importanti connessioni con i concetti fondamentali della meccanica statistica. La presenza di isole di regolarità immerse nel mare stocastico determina l'inapplicabilità del teorema ergodico all'intero spazio delle fasi. Le traiettorie nel mare caotico non possono mai approdare su isole di moto regolare e viceversa, definendo quindi una condizione di pseudoergodicità.
Completamente diverso è il caos dissipativo, di cui un tipico esempio è la seguente mappa di Henon (1976):
Lo spazio delle fasi di questo sistema può essere la parte di piano [0,1]×[0,1].
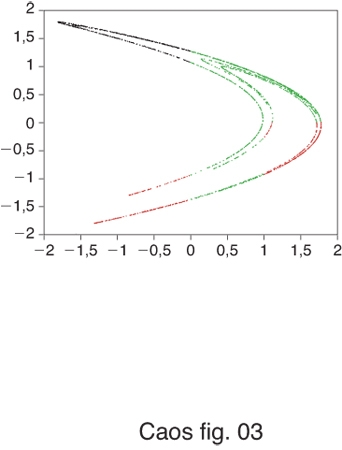
Per alcuni valori di K1 e K2, l'assenza di invarianti produce in questo caso una dinamica attraverso un processo di simultanea contrazione e dilatazione dell'intero spazio delle fasi verso una struttura frattale definita attrattore strano. Per l'iperbolicità, in questo caso non uniforme, del sistema, un generico punto all'interno dell'attrattore può essere considerato come l'intersezione di una direzione (stabile) dello spazio che si contrae e di una (instabile) che si espande, in modo da produrre un'estrema dipendenza dalle condizioni iniziali. Gli aspetti propriamente fisici e dinamici del sistema vengono quindi a essere espressi dalle proprietà geometriche e topologiche dell'attrattore. Uno dei risultati più interessanti è che la frequenza di visita di una traiettoria non è uniformemente distribuita sull'attrattore (fig. 3); si può in alcuni casi definire una misura invariante di probabilità, detta misura SRB (dalle iniziali di Sinai, Ruelle, Bowen) sul suo supporto frattale. In tal caso la sola dimensione di Hausdorff non è sufficiente a definire la struttura dell'oggetto; essa diventa parte di uno spettro di dimensioni, dette di Rènyi, e l'attrattore assume le caratteristiche di un multifrattale. Ne consegue che sebbene impredicibile, il sistema ammette una buona descrizione statistica del comportamento asintotico delle traiettorie sull'attrattore.
Il problema dell'esistenza e unicità di queste funzioni di probabilità è ancora uno dei temi aperti nella teoria dei sistemi dinamici, basti pensare che solo nel 1993 ne è stata dimostrata l'esistenza per la mappa di Henon. Lo sviluppo dell'analisi multifrattale ha aperto la strada alla cosiddetta termodinamica dei sistemi caotici. Uno dei risultati in questo campo è la possibilità di definire regioni di alta o bassa predicibilità sull'attrattore.
Con l'espressione edge of chaos (soglia di caoticità), coniata da C.G. Langton (1990), si indica l'insieme dei processi che accadono nell'attimo in cui la natura del sistema subisce la transizione ordine-disordine come risposta alla variazione del parametro di controllo. In questa transizione il sistema si autoorganizza tramite un'interazione globale e a tutte le scale dei suoi componenti. In sistemi di questo tipo la dinamica è spesso generata da semplici leggi matematiche come le mappe iterative. In relazione a tutto ciò, il fisico e premio Nobel M. Gell-Mann ha coniato il neologismo plectics (dal greco plektos, intrecciato), illustrando per mezzo di un solo termine il binomio semplicità-complessità. Uno dei campi di applicazione più interessanti di questa moderna scienza è la biologia, in cui la complessità si riscontra, per es., nella capacità di adattamento di un organismo rispetto al cambiamento di un parametro ambientale esterno.
Nel campo sperimentale, l'affermarsi della teoria del caos ha dato impulso allo studio di tecniche di analisi di segnali irregolari osservati in natura o rilevati da esperimenti in laboratorio. Tramite l'apparato teorico dei sistemi dinamici, la cosiddetta analisi non lineare di serie temporali affianca alla classica analisi di Fourier algoritmi numerici per l'identificazione e la quantificazione dei segnali caotici, insieme a tecniche di ricostruzione dell'attrattore del sistema. In questo campo un contributo è senza dubbio quello dello sviluppo di strumenti non lineari come le reti neurali e gli algoritmi genetici. Il considerevole lavoro svolto nell'ambito delle serie temporali si propone l'analisi di metodi utili a distinguere segnali caotici da segnali stocastici, che in concetti come quello della complessità algoritmica, propri della teoria dell'informazione, sono risultati essere un potente mezzo di ausilio teorico per la conoscenza di un sistema dinamico. Immaginando di descrivere una traiettoria tramite una stringa di numeri binari, una definizione di essa, detta di Kolmogorov-Chaitin, corrisponde alla lunghezza del minimo programma binario necessario a riprodurla. Dinamiche regolari, legate a sistemi integrabili hanno complessità algoritmica minima, a differenza dei sistemi stocastici con complessità proporzionale alla lunghezza della stringa. Si potrebbe quindi pensare che un calcolo della complessità algoritmica di serie temporali caotiche possa portare alla scrittura di un algoritmo universale di previsione delle stesse. G. Chaitin ha dimostrato l'impossibilità di tale costruzione in base al teorema di incompletezza di K. Gödel, aprendo nuovi orizzonti al dibattito epistemologico sulla intelligibilità dell'Universo. Molti fenomeni n aturali sono descritti da modelli matematici in cui coesiste un soggetto forzante esterno e una dissipazione interna. Da questo punto di vista, risvolti 'ingegneristici' dei sistemi caotici dissipativi trovano utilizzo in vari settori applicativi. Un esempio per tutti è la tecnica di previsioni meteorologiche denominata Ensemble Prediction System (EPS). Il matematico V.I. Arnol´d (1966) ha dimostrato, per modelli semplici di moti atmosferici, che l'incertezza delle previsioni numeriche è indipendente dalla potenza di calcolo degli elaboratori, ma è dovuta all'alta non linearità delle equazioni fluidodinamiche. Si ha quindi a che fare con un sistema caotico dissipativo in cui la struttura del cosiddetto attrattore meteorologico è comunque sconosciuta. La metodica dell'EPS si basa sull'esplorazione numerica dell'attrattore, effettuata tramite un insieme di previsioni che partono da condizioni iniziali dell'atmosfera prossime all'analisi della situazione meteorologica osservata. Il grado di divergenza delle traiettorie così generate permette di definire una probabilità sulla certezza della previsione. Un esempio eclatante di impredicibilità è stata la tempesta, denominata Lothar, abbattutasi in Europa alla fine del 1999 e assolutamente non prevista dai servizi meteorologici nazionali (fig. 4). La moderna visione dei sistemi dinamici caotici, nata come si è visto nel campo della meccanica classica, ha avuto interessanti estensioni nei campi della fisica moderna, come le teorie di campo e la meccanica quantistica.Nel campo della relatività generale, interessanti studi sulle condizioni iniziali e asintotiche nel tempo di modelli cosmologici come gli universi di Bianchi, sono stati condotti al fine di ricercare soluzioni caotiche per le equazioni classiche del campo gravitazionale di A. Einstein, e di cosmologie precedenti al Big Bang associate alla moderna teoria delle stringhe. Nel campo della teoria quantistica, la struttura profondamente diversa dalla meccanica classica rende particolarmente complesso il concetto di comportamento caotico. Il principio di indeterminazione di W.K. Heisenberg preclude la conoscenza 'puntuale' dello spazio delle fasi di un sistema e quindi delle condizioni iniziali di esso. Dal punto di vista della meccanica classica, immaginando di sostituire il concetto di traiettoria con il comportamento nel tempo della funzione d'onda descritto dall'equazione di Schrödinger, si può facilmente dimostrare la non esistenza del caos, inteso come separazione tra due traiettorie inizialmente vicine. Infatti, essendo l'operatore di evoluzione U per la funzione d'onda
un operatore unitario, ovvero U+U=1, si ha
Mentre da una parte la 'distanza' tra due pacchetti d'onda resterà costante nel tempo, dall'altra parte, nel contesto del paradigma quantistico, l'interpretazione probabilistica della funzione d'onda porta alla completa caoticità, intesa come mancanza di predicibilità, della meccanica quantistica. A questo paradosso si è ovviato cercando definizioni applicabili a sistemi dinamici in cui sono rilevanti entrambi gli effetti di non linearità e quantistici.
I sistemi più frequentemente studiati sono la controparte quantistica di sistemi caotici classici, di tipo hamiltoniano o dissipativo. Sistemi semiclassici di questo tipo rilevano comportamenti diversi dai sistemi regolari quantistici derivanti dai corrispettivi classici al variare del parametro di controllo. Uno degli aspetti più interessanti in questo campo è il diverso comportamento statistico dei livelli quantici di energia per sistemi regolari e caotici, che ha rivelato un inatteso legame tra il caos quantistico e l'affascinate campo della ricerca dei numeri primi.
Bibliografia
C.D. Murray, S.F. Dermott, Solar system dynamics, Cambridge-New York 1999.
M. Viana, Dynamical systems: moving into the next century, in Mathematics unlimited-2001 and beyond, ed. B. Engquist, W. Schmid, Berlin-New York 2001, pp. 1167-79.
T. Bhattacharya, S. Habib, K. Jacobs, The emergence of classical dynamics in a quantum world, in Los Alamos Science, 2002, 27, pp. 110-25.
M. Gell-Mann, Plectics: the study of simplicity and complexity, in Europhysics news, 2002, 1, pp. 17-20.
T.N. Palmer, Prediciting uncertainty in numerical weather forecasts, in Meteorology at the Millennium, ed. R.P. Pearce, San Diego 2002, pp. 3-13.
S.H. Strogatz, Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering, Cambridge (MA) 2002.
W.H. Zurek, Decoherence and the transition from quantum to classical - Revisited, in Los Alamos Science, 2002, 27, pp. 2-25.
J.C. Sprott, Chaos and time-series analysis, Oxford-New York 2003.
G.M. Zaslavsky, Hamiltonian chaos and fractional dynamics, New York 2005.
V. Pelino, Il caos nelle previsioni meteorologiche e climatiche, in Rivista di meteorologia aeronautica, 2006, 2.