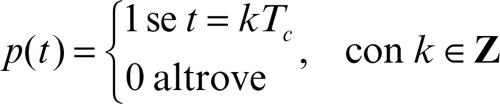funzione, campionamento di una
funzione, campionamento di una
funzione, campionamento di una nelle applicazioni tecniche della matematica, procedura che trasforma un segnale fisico di tipo analogico, quale per esempio un brano musicale, in una sequenza di byte trattabili da un apparato elettronico. Dal punto di vista matematico, un segnale analogico elementare è una funzione reale y = ƒ(x) definita e continua in un intervallo [a, b] ∈ R. Poiché un sistema elettronico, quale per esempio un lettore di cd, opera soltanto su valori discreti, occorre effettuare una conversione analogica-digitale (adc), in cui tale segnale analogico continuo sia trasformato in una successione di valori discreti yk = ƒ(xk), con k = 1, ..., n, in corrispondenza degli estremi di una partizione x1, x2, ..., xn di [a, b], con x1 = a e xn = b.
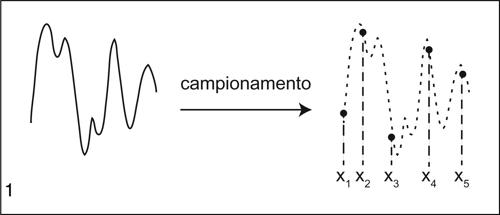
Il processo completo di conversione comprende tre fasi distinte e sequenziali: il campionamento della funzione di partenza, la quantizzazione dei valori campionati della funzione, la codifica digitale finale.
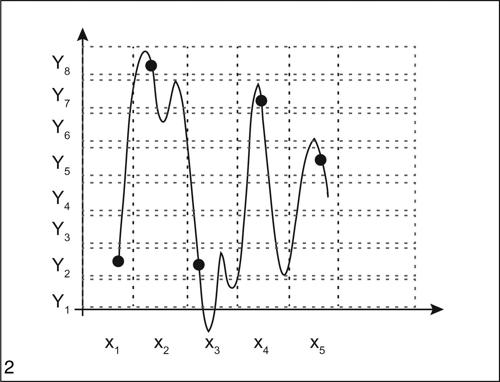
Il campionamento seleziona alcuni valori discreti della variabile indipendente. La quantizzazione dei valori della funzione considera una partizione y1, y2, ..., ym dell’immagine della funzione stessa, effettuando un’operazione di troncamento o di arrotondamento oppure di media tra gli estremi del valore assunto dalla funzione in ciascun sottointervallo [yk, yk+1] della partizione stessa. Tale operatore di quantizzazione Q(y) seleziona quindi un valore per ognuno di tali sottointervalli:
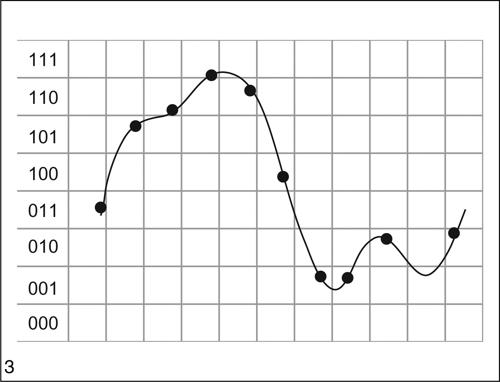
con k = 1, 2, ..., m − 1. La codifica digitale infine trasforma i valori così quantizzati in stringhe di 0 e 1 in codice binario, memorizzati dalla macchina in modo che possano successivamente essere elaborati.
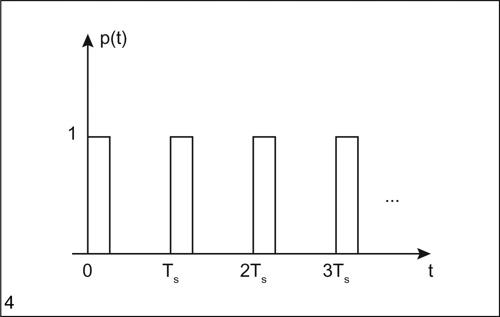
Il campionamento assume un ruolo particolare quando la funzione da campionare è un segnale analogico continuo dipendente dal tempo y = ƒ(t); in questo caso, per generare sottointervalli uguali, come partizione dell’asse temporale si considera il periodo di campionamento Tc, oppure la frequenza di campionamento ƒc = 1/Tc. Si genera così la successione dei valori campionati yc(t) = y(kTc). Un metodo per ottenere facilmente un campionamento periodico è quello di considerare una funzione periodica p(t), detta impulso periodico e definita per casi:
In tale modo il campionamento desiderato si realizza semplicemente moltiplicando la funzione da campionare per l’impulso periodico: yc(t) = y(t) ⋅ p(t).
