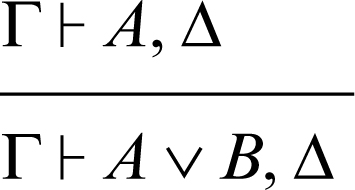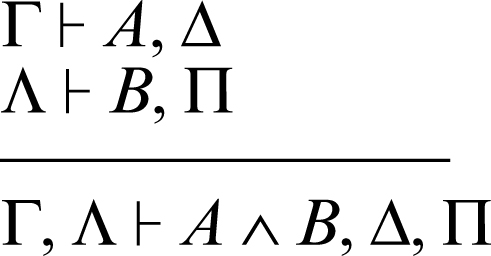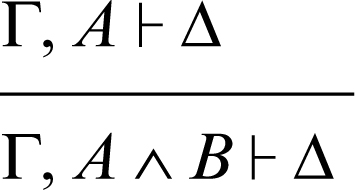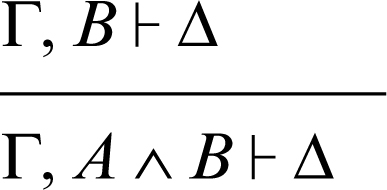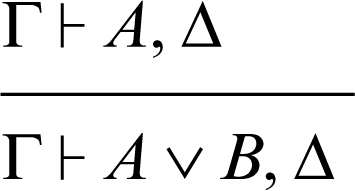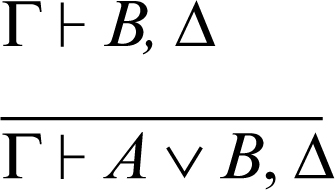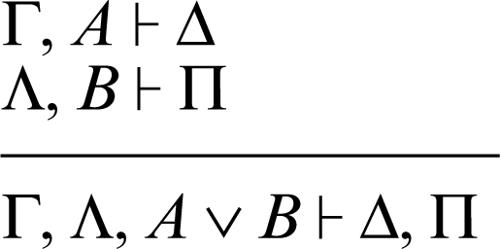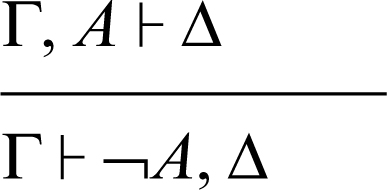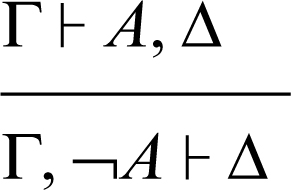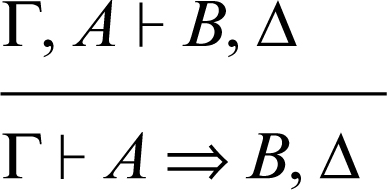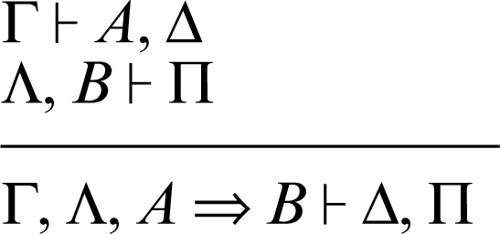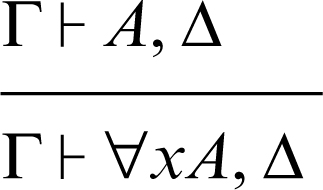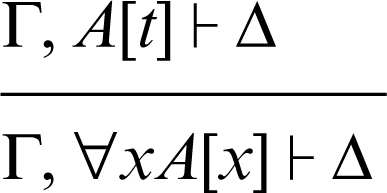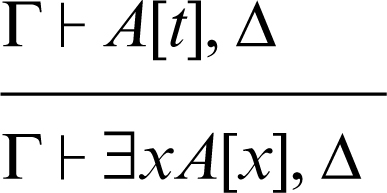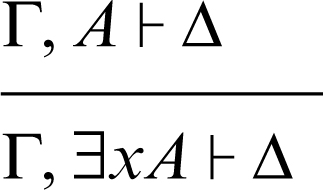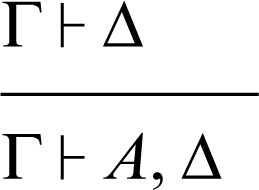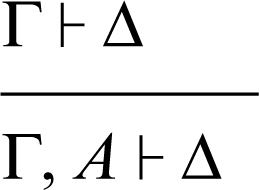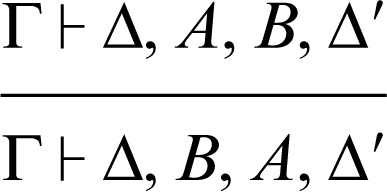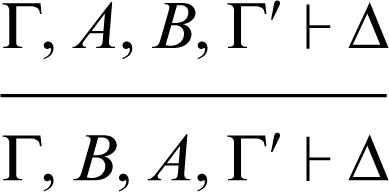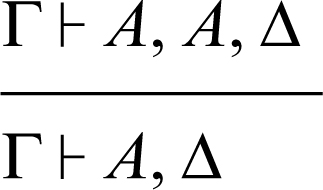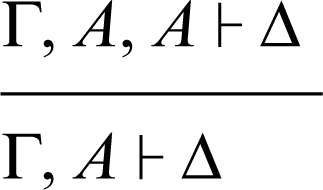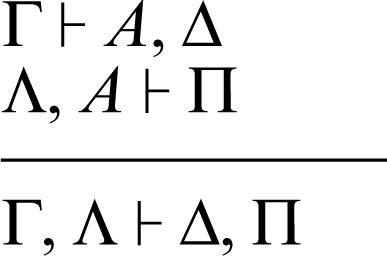sequenti, calcolo dei
sequenti, calcolo dei
sequenti, calcolo dei calcolo logico introdotto da G. Gentzen negli anni Trenta del xx secolo i cui elementi sono i sequenti, vale a dire espressioni del tipo Γ ⊢ Δ in cui Γ e Δ sono sequenze finite di formule ben formate di un linguaggio logico (→ enunciati, linguaggio degli; → predicati, linguaggio dei) e il simbolo Γ ⊢ Δ corrisponde alla seguente implicazione: «se tutte le formule di Γ (premesse) sono vere allora almeno una delle formule di Δ (conseguenze) è vera». Così definito, il sequente A1, ..., An ⊢ B1, ..., Bn equivale all’enunciato A1 ∧ ... ∧ An ⇒ B1 ∨ ... ∨ Bn. Il sequente rappresenta una relazione di deducibilità fra le premesse e le conclusioni; l’espressione Γ ⊢ Δ equivale quindi all’esistenza di una deduzione che porti dalle premesse Γ alle conseguenze Δ. Come negli altri calcoli logici, anche in questo caso sono presenti assiomi e regole di derivazione che consentono lo sviluppo del calcolo fornendo delle regole per la costruzione di una deduzione. In questo caso l’unico assioma è l’assioma identità che assicura la validità del sequente A ⊢ A, dove A è una qualsiasi formula ben formata e le regole di derivazione si dividono in regole logiche, regole strutturali e regola del taglio.
Regole logiche
Le regole logiche sono utilizzate per introdurre, a destra o a sinistra del simbolo di sequente, i → connettivi e i → quantificatori. Per esempio, la regola di introduzione del connettivo ∨ (disgiunzione) a destra del simbolo di sequente può essere rappresentata nel modo seguente:
La linea orizzontale indica che il sequente Γ ⊢ A ∨ B, Δ è stato dedotto dal sequente Γ ⊢ A, Δ. Di seguito sono riportate le regole logiche del calcolo dei sequenti, dove Π indica anch’esso una sequenza finita di formule.
• Congiunzione
introduzione della congiunzione a destra
introduzione della congiunzione a sinistra 1
introduzione della congiunzione a sinistra 2
• Disgiunzione
introduzione della disgiunzione a destra 1
introduzione della disgiunzione a destra 2
introduzione della disgiunzione a sinistra
• Negazione
introduzione della negazione a destra
introduzione della negazione a sinistra
• Implicazione
introduzione dell’implicazione a destra
introduzione dell’implicazione a sinistra
• Quantificatore universale
introduzione del quantificatore universale a destra
(in questa regola la variabile x non è una variabile libera nelle formule di Δ e Γ)
introduzione del quantificatore universale a sinistra
(in questa regola t rappresenta un qualsiasi termine del linguaggio e A[x] rappresenta la sostituzione della variabile x al posto del termine t)
• Quantificatore esistenziale
introduzione del quantificatore esistenziale a destra
(in questa regola t rappresenta un qualsiasi termine del linguaggio e A[x] rappresenta la sostituzione della variabile x al posto del termine t)
introduzione del quantificatore esistenziale a sinistra
(in questa regola la variabile x non è una variabile libera nelle formule di Δ e Γ).
Regole strutturali
Le regole strutturali sono la regola di indebolimento, che permette di aggiungere formule a sinistra o a destra del simbolo di sequente, indebolendo in tal modo le premesse o le conseguenze, la regola di scambio, che permette di permutare l’ordine delle formule che compaiono nelle premesse o nelle conseguenze, e la regola di contrazione, che permette di passare da due occorrenze della stessa formula nelle premesse o nelle conseguenze a una occorrenza sola di tale formula.
• Indebolimento
indebolimento a destra
indebolimento a sinistra
• Scambio
scambio a destra
scambio a sinistra
• Contrazione
contrazione a destra
contrazione a sinistra
Per esemplificare l’applicazione di alcune di queste regole si riporta la deduzione del sequente ⊢ (corrispondente a una tautologia nel calcolo degli enunciati) a partire dall’assioma A ⊢ A:
Particolare importanza riveste nel calcolo dei sequenti la regola del taglio che permette di eliminare, nel corso di una deduzione, una formula che appare sia nelle conseguenze di un sequente sia nelle premesse di un altro sequente.
• Regola del taglio
La regola del taglio è l’unica regola che consente l’eliminazione di una formula da un sequente: nel sequente risultante non c’è infatti più traccia della formula A. Da ciò discende che una deduzione di un sequente Γ ⊢ Δ in cui venga fatto uso della regola del taglio è una dimostrazione “non meccanicistica” in quanto non è possibile stabilire in modo automatico i passaggi necessari per dedurre il sequente Γ ⊢ Δ a partire dall’assioma identità. Tuttavia, grazie al teorema di eliminazione del taglio (→ taglio, regola del) è possibile associare a ogni deduzione di un sequente Γ ⊢ Δ una deduzione dello stesso sequente in cui non si faccia uso della regola di taglio. Questa possibilità rende le deduzioni del calcolo dei sequenti paragonabili a procedure algoritmiche e stabilisce un legame fra la teoria della dimostrazione e l’informatica teorica. Tale legame è sancito dall’isomorfismo di → Curry-Howard.
Il calcolo dei sequenti è stato applicato non soltanto alla logica classica, ma anche ad altri tipi di logica quali la → logica intuizionista, la → logica minimale e la → logica lineare, effettuando opportune modifiche sulla struttura dei sequenti ed eliminando alcune regole strutturali.