birapporto

birapporto

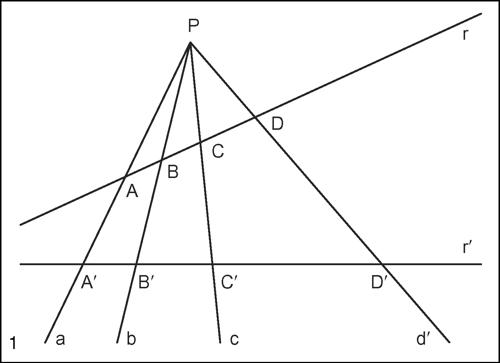
birapporto nella geometria proiettiva, il birapporto di quattro punti allineati A, B, C, D, disposti sulla retta orientata, è il numero reale

essendo AC, BC, AD, BD le misure con segno delle distanze tra i rispettivi punti, espresse in un’unità di misura arbitraria. Il birapporto è generalmente indicato con la scrittura (ABCD). Dalla sua definizione segue che esso risulta indipendente dall’orientamento della retta, dalla scelta dell’origine e dell’unità di misura. Se A e B precedono o seguono C e D oppure sono entrambi compresi tra C e D o ancora se C e D sono entrambi compresi tra essi, il birapporto ha segno positivo. Se A, B, C,D si alternano ha segno negativo. Si ha inoltre:

• (ABCD) = 0 se A = C oppure B = D;

• (ABCD) = 1 se A = B oppure C = D;

• (ABCD) tende a infinito se B tende a C oppure A tende a D;

• (ABCD) ≠ 0 e (ABCD) ≠ 1 se A, B, C, D sono quattro punti distinti.

Se si ha (ABCD) = −1, ai quattro punti si dà il nome di → quaterna armonica. Modificando l’ordine in cui vengono presi i quattro punti, si ottengono 24 diverse sequenze (permutazioni), ma si hanno soltanto sei diversi valori del birapporto k.

Poiché il rapporto semplice di tre punti allineati è dato da (ABC) = AC/BC, si ha

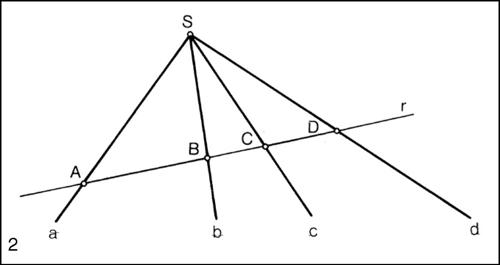
Il birapporto è quindi il rapporto di due rapporti semplici. La definizione di birapporto si estende a quattro rette di un fascio, nel modo che segue

Il birapporto delle quattro rette, così definito, è uguale al birapporto dei rispettivi quattro punti in cui esse sono intersecate da una qualsiasi retta del piano. Si ha infatti (abcd) = (ABCD) = (A′B′C′D′). Il birapporto di quattro elementi è invariante per trasformazioni proiettive, mentre non si conserva in una trasformazione affine. Come nozione propria della geometria proiettiva, esso può essere applicato anche a punti e rette improprie, poiché questi oggetti, in ambito proiettivo, non sono distinti da punti e rette propri. Il birapporto risulta inoltre invariante per inversioni circolari. Si osservi infine che la nozione di birapporto può essere estesa anche a quattro punti appartenenti a una conica. In tal caso esso è definito come il birapporto delle corrispondenti quattro rette che proiettano i punti dati da un punto qualsiasi della conica stessa.

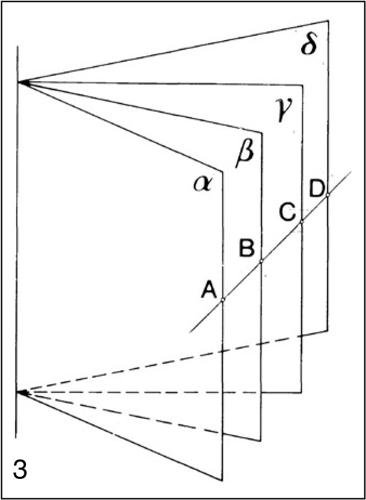
Il birapporto di quattro piani di un fascio è il birapporto dei quattro punti intersezione con una retta sghemba rispetto all’asse del fascio.