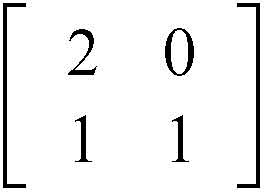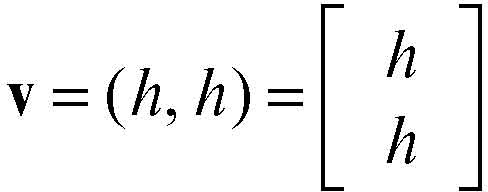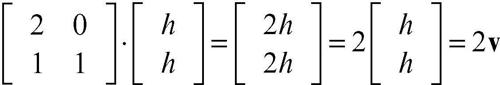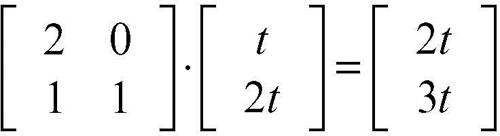autovettore
autovettore
autovettore vettore non nullo che non cambia direzione in una trasformazione lineare invertibile. In generale, una trasformazione di uno spazio vettoriale in sé modifica modulo, direzione e verso dei vettori; sotto certe condizioni è però possibile che alcuni vettori cambino solo di modulo e non di direzione; essi quindi si trasformano secondo un fattore di proporzionalità, cioè attraverso la moltiplicazione per uno scalare, detto autovalore, cui l’autovettore è associato. In una affinità del piano, se m rappresenta una direzione invariante, ogni vettore di coefficiente angolare m − e quindi di componenti (h, hm) con h ∈ R0 − è un autovettore. Per esempio, data la trasformazione affine del piano con punto unito l’origine e definita dalla matrice
una sua direzione invariante è m = 1. Si ha infatti che ogni vettore v con tale direzione, cioè
ha per trasformato il vettore
cioè un multiplo del vettore stesso. Un qualsiasi vettore con diversa direzione, per esempio w = (t, 2t), ha per trasformato
che non è multiplo di w. Il fattore k = 2 rappresenta il rapporto di dilatazione lungo la direzione m = 1 (per una trattazione più generale → autovalore).