angoloide

Enciclopedia della Matematica (2013)

angoloide


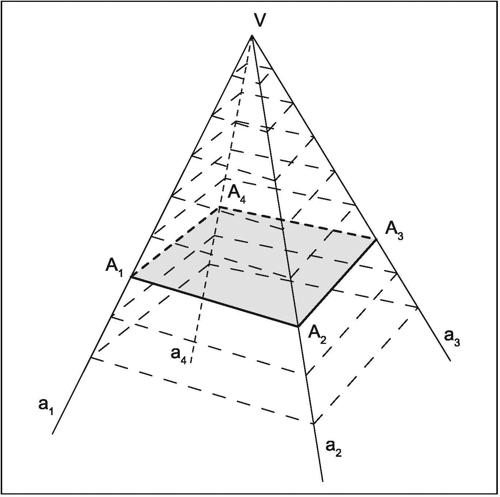
angoloide una delle generalizzazioni possibili del concetto di angolo nello spazio tridimensionale (per altre generalizzazioni vedi → diedro, → sterangolo). Dati un poligono convesso A1A2 ... An e un punto V non appartenente al piano del poligono, l’angoloide è la regione convessa di spazio limitata dagli angoli

formula

Il punto V è il vertice dell’angoloide, gli angoli

METODO DELL’ATTRATTORE

sono le sue facce, le semirette VA1,VA2,…, VAn sono i suoi spigoli. Ciascuno spigolo è origine di un diedro formato da due facce consecutive. In un angoloide la somma delle facce è minore di un angolo giro; infatti se la somma delle ampiezze di tali facce fosse uguale a 360°, l’angoloide si «appiattirebbe» degenerando in un piano e il suo vertice risulterebbe appartenere al piano del poligono A1A2 ... An, a partire dal quale esso è definito. L’ampiezza di ciascuna faccia è minore della somma delle ampiezze delle altre. La totalità delle facce costituisce la superficie dell’angoloide. Se le facce sono tutte uguali, l’angoloide si dice regolare. In un angoloide regolare i piani bisettori degli angoli diedri passano tutti per una stessa retta detta asse dell’angoloide. Un angoloide individuato da n spigoli, e quindi con n facce, si chiama n-edro (ennaedro) indefinito.

ANGOLOIDE

Vedi anche
spigolo Nella geometria elementare, ciascun lato dei poligoni che costituiscono un poliedro (s. del poliedro), ovvero ciascun lato degli angoli (facce) di un angoloide (s. dell’angoloide), ovvero la retta da cui escono i due semipiani di un diedro (s. del diedro). Lo s. di regresso è la linea sghemba cui sono ... vertice In geometria, il punto d’incontro dei lati di un poligono o il punto in cui concorrono spigoli e facce di un poliedro, o di un angoloide. In una conica, si chiama v. ognuno dei punti d’incontro della conica stessa con un suo asse. In geometria differenziale, v. di una linea, ogni punto di essa nel quale ... diedro Ciascuna delle due parti in cui lo spazio è diviso da due semipiani uscenti da una stessa retta. I due semipiani si dicono le facce, la retta lo spigolo o costola del diedro (➔ angolo). radianza In fisica, flusso di radiazione per unità di angolo solido e di area della sorgente. La grandezza fisica r. energetica (detta anche brillanza e la cui denominazione ISO è radiance) è il rapporto tra il flusso di radiazione per unità di angolo solido in una data direzione (intensità di radiazione) e l’area ...
Tag
Vocabolario
angolòide
angoloide angolòide s. m. [comp. di angolo e -oide]. – Tipo di angolo solido, costituito dalla parte di spazio che si ottiene dall’intersezione di almeno tre diedri i cui spigoli passano per uno stesso punto: a. triedro, tetraedro.
tetraèdro
tetraedro tetraèdro s. m. e agg. [dal gr. τετράεδρον, comp. di τετρα- «tetra-» e -εδρος «-edro»]. – 1. a. s. m. Il più semplice dei poliedri, che ha 4 vertici, 6 spigoli, 4 facce triangolari, e può essere pensato come una piramide a base...