angolo
angolo
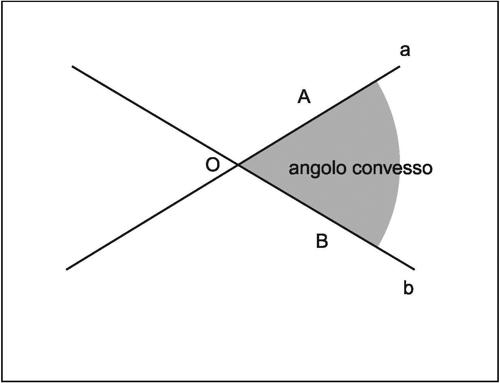
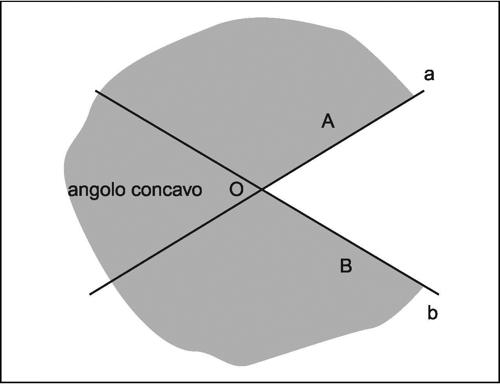
angolo parte di piano compresa tra due semirette (i lati dell’angolo) che hanno origine nello stesso punto (detto vertice dell’angolo). In termini insiemistici l’angolo può anche essere definito come intersezione o unione di due semipiani individuati da due rette non parallele: l’intersezione definisce un angolo convesso (angolo non contenente i prolungamenti dei lati), l’unione definisce un angolo concavo (angolo contenente i prolungamenti dei lati). Due distinte semirette, se non appartengono alla stessa retta (nel cui caso delimitano due angoli piatti) individuano quindi due angoli, l’uno concavo e l’altro convesso. Se O è il vertice dell’angolo e A e B due punti qualunque sui lati, rispettivamente indicati con a e b, entrambi gli angoli sono indicati con AÔB oppure aÔb.
Se i lati dell’angolo sono perpendicolari, l’angolo convesso da essi individuato è detto angolo retto; se i lati appartengono alla stessa retta ma non coincidono, essi individuano due semipiani, ciascuno dei quali è detto angolo piatto; se i due lati coincidono, l’angolo convesso individuato si riduce all’angolo nullo, mentre l’angolo concavo coincide con tutto il piano e prende il nome di angolo giro. L’angolo acuto è un angolo minore dell’angolo retto; l’angolo ottuso è un angolo convesso maggiore dell’angolo retto.
Due angoli possono essere, rispetto alla loro posizione, consecutivi, adiacenti, opposti al vertice (→ angoli associati (per posizione)). Rispetto alla loro somma, possono essere complementari, supplementari, esplementari (→ angoli associati (per ampiezza)). Particolari coppie di angoli sono quelle formate da due rette tagliate da una trasversale: gli otto angoli che ne risultano, presi a coppie, assumono nomi diversi a seconda della loro posizione reciproca (→ angoli associati (rispetto a due rette tagliate trasversalmente)).
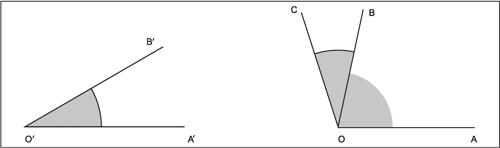
La misura di un angolo è espressa in gradi o in radianti (→ angolo, ampiezza di un). L’angolo somma di due angoli consecutivi è l’angolo formato dai due lati non comuni e contenente il lato comune. L’angolo somma di due angoli AÔB e A′Ô′B′ non consecutivi è l’angolo AÔC ottenuto disponendo un angolo BÔC = A′Ô′B′ come consecutivo ad AÔB.
Analogamente, la differenza di angoli (di cui il primo maggiore del secondo) può essere effettuata riportando un lato dell’angolo minore a coincidere con quello dell’angolo maggiore in modo che sia in esso contenuto e considerando quindi l’angolo individuato dai due lati non coincidenti. Può accadere che sommando due angoli si superi l’angolo giro, cioè si venga a coprire il piano più di una volta: ciò rende necessario estendere il concetto di angolo e considerare angoli maggiori dell’angolo giro, che sono detti angoli impropri; gli angoli compresi entro l’angolo giro sono perciò detti talvolta angoli propri. La necessità di considerare angoli maggiori dell’angolo giro risulta anche da un altro modo di intendere l’angolo, come espressione di una rotazione: un angolo AÔB si può infatti pensare come descritto da una semiretta mobile r, di origine O, che partendo da una posizione iniziale (primo lato dell’angolo), ruota intorno al vertice, in un determinato verso, fino a una qualunque altra posizione (secondo lato dell’angolo). Ciò consente di considerare uguali, ma di segno opposto i due angoli AÔB e BÔA: il primo va pensato come descritto dalla semiretta OA che ruota fino a sovrapporsi alla semiretta OB, il secondo come descritto, nel verso opposto, dalla semiretta OB che ruota fino a coincidere con la semiretta OA. Se si fissa come verso positivo della rotazione nel piano il verso antiorario, l’ampiezza di AÔB risulta positiva o negativa a seconda che OA, per descrivere l’angolo, debba ruotare in senso antiorario o in senso orario. Si è così fissato un orientamento e in tale caso si parla di angolo orientato. Di norma, in geometria analitica e in trigonometria gli angoli sono orientati.
Angoli particolari in un cerchio sono quelli che hanno il vertice nel centro (→ angolo al centro) o in un punto della circonferenza (→ angolo alla circonferenza). Nello spazio tridimensionale sono rilevanti l’→ angolo tra due piani e l’→ angolo tra retta e piano. Per le generalizzazioni possibili del concetto di angolo nello spazio tridimensionale si vedano le voci: → angoloide, → diedro, → sterangolo.