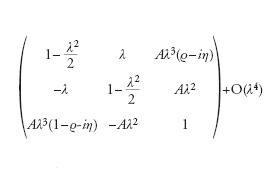angolo di mescolamento

angolo di mescolamento

seguente

[FNS] [FPE] Angolo che nel Modello Standard della fisica delle particelle, nell’ambito delle interazioni elettrodeboli, compare nella matrice unitaria V_ΧΚΜ di Cabibbo, Kobayashi e Maskawa che descrive il cambiamento di base tra i quark con definito isospin debole e i quark con massa definita. Questa matrice fu introdotta nel 1963 da Nicola Cabibbo e fu generalizzata per tre famiglie di quark dieci anni dopo da Makoto Kabayashi e Toshihide Maskawa, i quali hanno ottenuto il Nobel per la fisica nel 2008. In effetti esistono tre quark di tipo up, con terza componente dell’isospin debole uguale a +1/2, u (up), c (charm) e t (top) e tre quark di tipo down, con terza componente dell’isospin debole uguale a −1/2, d (down), s (strange) e b (bottom). Le interazioni deboli da corrente carica, mediate dai bosoni di gauge W^± fanno passare da un quark di tipo up a uno di tipo down con emissione di un W^±. Per es., un quark u con massa definita può emettere un W⁺ e trasformarsi in un quark di tipo down: u→W⁺+d′. Il quark finale d′, di tipo down, non sarà in generale un quark a massa definita, ma una sovrapposizione di stati d, s e b di massa definita. Similmente s′ e b′ appaiono nello stato finale delle transizioni iniziate da c e t, rispettivamente (c e t hanno massa definita, mentre s′ e b′ sono sovrapposizioni di d, s e b a massa definita). La matrice unitaria V_ΧΚΜ fa passare dalla base D′ – un vettore colonna con componenti (d′,s′,b′) – degli stati a interazione debole definita alla base D (d,s,b) degli stati a massa definita: D′=V_{ΧΚΜ D.} In generale una matrice unitaria 3×3 dipende da 9 parametri reali. Ma le fasi relative degli stati dei 6 quark up e down non hanno significato fisico. Quindi V_ΧΚΜ dipende da 4 parametri fisici reali. Questi sono 3 angoli (detti appunto di mescolamento) e una fase δ. Empiricamente gli angoli di mescolamento sono piccoli cosicché VΧΚΜ è quasi diagonale. Approssimativamente una parametrizzazione semplice di V_ΧΚΜ dovuta a Lincoln Wolfenstein è la seguente:

dove gli angoli di mescolamento sono senθ_C=λ, senθ^₂₃=Aλ2 e senθ₁₃ e^ιδ=Aλ³(ϱ−iη). θ₁₂=θ_C è l’angolo di Cabibbo. Dall’esperimento si hanno i seguenti valori:

λ=0,2258±0,0014,

A=0,818±0,016,

ϱ=0,164±0,029,

η=0,340±0,017

(il valore di η differente da zero comporta la violazione di CP).

→ Interazioni fondamentali