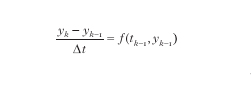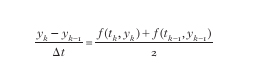ANALISI NUMERICA

Analisi numerica

L'a. n. è una branca della matematica che si occupa di individuare, analizzare e implementare algoritmi per la risoluzione approssimata di problemi matematici in genere, che possono scaturire da pure speculazioni, da reali esigenze di ricerca, o da simulazioni in campo tecnologico finalizzate alla progettazione di dispositivi complessi.

Benché la nascita ufficiale dell'a. n., come disciplina a sé stante, si possa far risalire agli anni Cinquanta del Novecento, con l'avvento e lo sviluppo dei primi calcolatori elettronici, le origini sono sicuramente più remote e trovano radici nell'antichità greca. Già nella seconda metà del Seicento, mentre il calcolo differenziale muoveva i primi passi, si manifestò immediatamente l'esigenza di determinare le soluzioni delle equazioni che venivano generate nello studio di certi fenomeni fisici. Essendo la via del calcolo esplicito molto spesso impraticabile, furono sviluppate nei secoli successivi opportune tecniche di approssimazione, tanto che tuttora alcuni algoritmi prendono il nome di B. Cavalieri, I. Newton, L. Eulero, C. Gauss, C. Jacobi, P. Chebyshev, C. Lanczos, e altri celebri scienziati del passato che hanno orientato la loro ricerca verso le scienze applicate.

Mentre i modelli, proposti per spiegare gli eventi naturali, divenivano via via più complessi, le metodologie dell'a. n. si adattavano alla loro evoluzione. I calcoli venivano tuttavia svolti a mano e, solo più tardi, con strumenti meccanici. Finché, nel 1947, grazie anche al contributo di J. von Neumann, fu creato il primo computer totalmente elettronico, proprio con la finalità di risolvere in modo veloce, mediante il calcolo approssimato, problemi che altrimenti avrebbero richiesto un ingente lavoro umano. Questo segnò la svolta e l'a. n. crebbe, non solo con lo scopo di risolvere direttamente problemi sempre più raffinati e complicati, ma si organizzò in sottosettori, ciascuno dei quali forma tutt'oggi oggetto di studi teorici approfonditi. Ciascun settore ha successivamente avuto uno sviluppo indipendente, sebbene tutti siano potenzialmente necessari per affrontare le grandi sfide della moderna tecnologia.

Stime dell'errore

Prima di esaminare qualche problematica è bene fare alcune considerazioni generali. Dato un problema, occorre per prima cosa individuare il metodo che più si adatta alla sua risoluzione, cercando fra quelli noti oppure creandone opportunamente di nuovi. È essenziale che l'algoritmo sia eseguibile tramite un numero finito di operazioni (in linea di massima: somme e sottrazioni, moltiplicazioni e divisioni, confronti fra numeri). Alla fine del calcolo, la cui durata dipende da molte circostanze, si perviene a quella che viene detta soluzione numerica (o approssimata) del problema, che consiste in un numero finito, per quanto grande esso possa essere, di valori numerici. Per poter fare affidamento sui valori trovati è importante fornire le cosiddette stime dell'errore. Le stime danno un limite superiore all'errore che si commette prendendo per buoni i valori calcolati al posto di quelli esatti (non disponibili), che deriverebbero dalla perfetta risoluzione del problema all'origine. Accade non di rado che i valori determinati con un certo algoritmo, per quanto ragionevole esso sia, non abbiano nulla a che fare con i rispettivi valori esatti. Molti di questi esempi sono di notevole ausilio didattico, in quanto mostrano come possa capitare, senza un'adeguata preparazione teorica, di giungere a valutazioni del tutto erronee e, pertanto, insignificanti. Lo studio delle stime dell'errore, parte indispensabile dell'a. n., è di conseguenza un fattore fondamentale nella pratica.

Al fine di chiarire la situazione, diamo di seguito un esempio concreto. Il problema è quello di determinare la radice quadrata del numero 7. La scrittura simbolica √7 non è d'ausilio in quanto indica la soluzione solo formalmente, senza essere efficace ai fini pratici. Il quesito può essere riformulato chiedendo di cercare la soluzione positiva dell'equazione di secondo grado: x²−7=0.

Fra le svariate tecniche a disposizione, quella che porta il nome di Newton consiste nel partire da un valore arbitrario positivo, e procedere nel calcolo dei successivi termini tramite l'algoritmo:

Formula

Dato il valore x_n−1, si può perciò calcolare il successivo valore x_n usando le classiche quattro operazioni. Si dimostra che, al crescere del numero di iterazioni n, il valore x_n si avvicina sempre più a √7, cioè la successione x_n−√7 tende a zero per n tendente a infinito. Qualunque calcolatore, adeguatamente programmato, è ora in grado di valutare x_n, anche per degli indici n molto grandi. Il fatto che la stesura di un algoritmo analogo, per il calcolo di √2, sia attribuita a Erone di Alessandria (1° sec. d.C. circa), pone in rilievo quanto siano antiche le origini dell'analisi numerica. Ricordiamo che x_n è l'unica quantità che si ha a disposizione dopo il calcolo, per cui è cruciale sapere quanto essa sia distante dal valore incognito √7. Al proposito, sfruttando conoscenze di analisi matematica, si è in grado di dimostrare la stima dell'errore:

Formula

per un dato x₀>√7. Noti x₀ e x_n, queste disuguaglianze ci permettono di controllare, dopo n passi, la distanza fra x_n e √7, pur non conoscendo esplicitamente quest'ultimo valore. In altre parole, la stima dell'errore consente di dedurre quante cifre decimali di x_n siano affidabili. Nel caso che il grado di accuratezza prestabilito non sia raggiunto, si potrà proseguire reiterando l'algoritmo.

Errori di arrotondamento. - Nel calcolo di x_n emerge subito un altro problema tipico dell'a. n., cioè quello relativo allo studio degli errori prodotti dalla macchina calcolatrice, che, per quanto accurata possa essere, è costretta ad operare solo con numeri la cui rappresentazione decimale è finita. Accade quindi che, durante la procedura di calcolo (per es. in una moltiplicazione), venga eseguito un arrotondamento del risultato. Questo errore, introdotto automaticamente, può propagarsi e accumularsi ad altri errori nelle operazioni successive; il risultato finale risulta pertanto inevitabilmente affetto, in misura più o meno consistente, da perturbazioni legate all'accuratezza con la quale la macchina è in grado di portare a termine ciascuna operazione intermedia. Un'analisi teorica della propagazione degli errori, nell'ambito dei diversi algoritmi, permette di conoscere quante cifre decimali del risultato x_n siano significative, valutando il rischio che da un certo punto in poi il calcolo sia stato inficiato dal modus operandi della macchina. Si possono fare esempi di algoritmi per i quali una non elevata precisione nel calcolo introduce errori di tale entità, da rendere i risultati finali del tutto inutilizzabili.

Alcuni temi che vengono affrontati in questo settore dell'a. n. comprendono: l'approssimazione dei numeri reali con numeri di macchina, i concetti di overflow e underflow, gli errori assoluti e relativi e la loro propagazione, il concetto di condizionamento di un problema, gli algoritmi stabili e la complessità computazionale.

Risoluzione di sistemi di equazioni

Quello trattato precedentemente è un caso particolare del problema più generale di trovare i valori incogniti x per i quali una data funzione f si annulla, cioè f(x)=0. Per quanto riguarda l'approssimazione di detti valori si può attingere da numerosi algoritmi, le prestazioni dei quali differiscono alquanto. In genere ha interesse individuare quello che fornisce la soluzione più accurata con il minimo sforzo, che viene misurato in proporzione al numero di operazioni elementari che risultano necessarie a sviluppare l'intero algoritmo. Altri fattori potrebbero tuttavia contribuire alla scelta. Si tenga pure presente che la velocità dei calcolatori disponibili al giorno d'oggi consente di svolgere calcoli in tempi estremamente brevi.

Tra i metodi più comuni per la ricerca degli zeri di funzioni di una variabile si annoverano il metodo di bisezione, quello di Newton-Raphson, e quello delle secanti. Tecniche più specifiche possono venire utilizzate nel caso in cui la funzione f sia un polinomio e sono valide spesso anche per la determinazione delle radici complesse.

La questione si complica quando si vuole affrontare la ricerca degli zeri di sistemi di equazioni. Un esempio in due variabili è dato dalla risoluzione contemporanea delle due equazioni f(x,y)=0, g(x,y)=0, dove f e g sono funzioni assegnate. Si pensi che i problemi che vengono affrontati nelle odierne applicazioni possono arrivare anche a milioni di equazioni da risolvere simultaneamente. Le tecniche adottate sono sovente opportune estensioni di quelle usate per il caso di una sola equazione, come per es. il metodo di Newton. La scelta del metodo è fondamentale, in quanto i tempi di esecuzione dell'algoritmo, al fine di assicurare una determinata accuratezza, variano di molto a seconda dei casi. I problemi possono essere così impegnativi da mettere in difficoltà le più veloci macchine di calcolo. A ciò va aggiunto che, data la quantità di operazioni necessarie, il rischio di eccessiva perturbazione dei risultati, a causa degli errori di arrotondamento, non è un fattore da trascurare.

Algebra lineare numerica. - Nella risoluzione di sistemi di equazioni è norma distinguere il caso lineare da quello non lineare. Nel primo, il sistema può venir scritto introducendo una matrice quadrata M (con un numero n di righe, pari al numero di equazioni). Per es., per n=2, un sistema lineare si scrive come:

Formula

e in forma matriciale come:

Formula

dove la matrice M e i valori b₁ e b₂ sono assegnati, mentre le componenti del vettore (x,y) costituiscono le incognite. Per il trattamento numerico di questi problemi, sono disponibili vari algoritmi, che verranno succintamente descritti fra breve.

Il secondo caso, quello non lineare, viene solitamente affrontato attraverso la creazione di una successione di sistemi lineari, riconducendosi quindi al caso precedente. La successione è infinita, ma viene opportunamente troncata, sulla base di informazioni deducibili da stime dell'errore. A ogni iterazione occorre però risolvere un sistema lineare, che potrebbe essere anche di grandi dimensioni e la cui matrice viene ogni volta modificata. È evidente che la messa in opera di siffatti algoritmi comporta un notevole dispendio di risorse. I problemi con molte incognite richiedono esperienza e specializzazione, anche perché, come sempre accade in a. n., tecniche diverse applicate allo stesso sistema di equazioni possono portare a risultati estremamente diversificati, sia per quanto riguarda l'accuratezza sia per i tempi di esecuzione.

Nel caso lineare è d'uso distinguere fra metodi di tipo diretto e di tipo iterativo. Nell'ambito dei metodi diretti, le incognite vengono calcolate esattamente (se si trascurano gli errori introdotti dal calcolatore), mediante un algoritmo che consta di un numero finito di operazioni. Il capostipite di queste tecniche è sicuramente il metodo di eliminazione di Gauss. A partire da esso sono disponibili infatti innumerevoli varianti. Riguardo al semplice esempio relativo a n=2, nell'implementazione del metodo di Gauss, supposto m₂₁≠0, si sottrae dalla prima equazione la seconda moltiplicata per m₁₁/m₂₁, ricavando:

Formula

dove x non compare più. Da questa scrittura si ottiene dunque l'incognita y. Successivamente, sfruttando ancora la prima equazione, essendo ormai nota y, si deduce il valore di x.

Per sistemi di dimensioni più grandi (n>2), le operazioni si complicano. L'idea rimane comunque la medesima e si basa sul calcolo di ciascuna incognita separatamente, attraverso opportune combinazioni delle equazioni di partenza, fatte in modo che il nuovo sistema risultante sia di forma 'triangolare' e lasci inalterate le soluzioni. Il numero di operazioni elementari necessarie per portare a compimento l'algoritmo è proporzionale al cubo della dimensione della matrice (n³). In certe circostanze, questa tecnica, per quanto elementare e sicura, può essere giudicata relativamente onerosa. Le sue varianti sfruttano particolari (addizionali) proprietà della matrice M al fine di risparmiare sul numero di operazioni.

Si parla pertanto di matrici sparse (quelle aventi molti coefficienti m_ij nulli) o con particolare struttura (tridiagonale, pentadiagonale, a banda, simmetrica, ecc.). Alcune delle tecniche alternative, note come metodi di fattorizzazione, sfruttano la struttura di M, non solo per ridurre i tempi di calcolo, ma anche per economizzare memoria. Per matrici simmetriche e definite positive un metodo molto sfruttato è quello di Cholesky.

Un'altra famiglia di metodi diretti per la risoluzione dei sistemi lineari poggia sui cosiddetti metodi di ortogonalizzazione. Tra questi si possono citare quelli di Householder e di Schmidt. Molte delle tecniche disponibili per la risoluzione di un sistema lineare si prestano anche al calcolo degli autovalori, e dei relativi autovettori, della corrispondente matrice M.

Nei metodi di tipo iterativo, si costruisce, a partire da uno o più vettori iniziali assegnati, una successione di vettori in modo che questa converga, componente per componente, al vettore incognito. L'algoritmo non si conclude quindi in un numero finito di passi, ma viene arrestato a una certa iterazione, quando il vettore approssimante non dista dal vettore esatto più di una certa tolleranza. Ciò viene deciso, senza ovviamente conoscere la soluzione esatta, attraverso le consuete stime dell'errore, ricavate per via teorica. Se l'accuratezza non è una delle prerogative del calcolo, il fatto che ci si possa avvicinare a piacere alla soluzione esatta permette di interrompere il procedimento in qualsiasi momento, con un conseguente risparmio sui tempi di esecuzione. Questo non è possibile con un metodo diretto il quale fornisce i valori delle incognite solo dopo aver portato a termine l'intero algoritmo. Fra i metodi iterativi più in voga ricordiamo quelli di Jacobi, Gauss-Seidel, di rilassamento. Altre tecniche sono disponibili per la ricerca di autovalori e autovettori.

Vi è infine un'altra classe di metodi di tipo iterativo per la risoluzione di sistemi di equazioni lineari, la cui teoria poggia sulla costruzione di opportune basi di vettori ortogonali. Il capostipite è il metodo del gradiente coniugato, che, nel caso di matrici simmetriche e definite positive, produce anche la soluzione esatta in un numero finito di iterazioni (a meno degli errori introdotti dalla macchina). Esso e le sue varianti sono forse tra le tecniche più usate nelle applicazioni, fornendo approssimazioni di buona accuratezza a costi competitivi.

Particolare rilevanza, nello studio teorico di tutte le suddette tecniche di calcolo, ha il concetto di condizionamento di una matrice. Le matrici che in qualche modo vengono definite malcondizionate, sono quelle che più creano difficoltà, sia perché la velocità di convergenza degli algoritmi viene ridotta in loro presenza, sia perché sono maggiormente sensibili alla propagazione degli errori di arrotondamento. È prassi applicare ai sistemi malcondizionati opportuni 'precondizionatori', al fine di renderli più idonee all'utilizzo.

Ottimizzazione lineare e non lineare

Capita di frequente nelle applicazioni di dover minimizzare (o massimizzare) una data funzione. Per es., in programmazione matematica, viene richiesto di realizzare il minimo (o il massimo) di una certa 'funzione obiettivo', quando le variabili sono soggette a opportuni vincoli lineari di uguaglianza o disuguaglianza. La programmazione lineare studia il caso in cui la funzione obiettivo è lineare; la programmazione non lineare studia il caso generale, incluso quello di notevole rilievo in cui la funzione obiettivo è quadratica. Le principali applicazioni si incontrano in ingegneria gestionale, in economia e nei problemi di controllo in generale. Non va dimenticato che una delle discipline che più si avvicinano allo studio di simili problematiche è la ricerca operativa.

Per quanto riguarda l'approccio numerico, il metodo del simplesso è la tecnica iterativa fra le più note in programmazione lineare per il calcolo della soluzione ottimale. L'algoritmo si basa sul fatto che, in opportune ipotesi, la configurazione ottimale è ottenuta in corrispondenza di un vertice del poliedro che descrive il cosiddetto dominio di ammissibilità. Il metodo ha numerose varianti e generalizzazioni. Sono disponibili inoltre altre tecniche più efficaci dal punto di vista delle prestazioni (per es., i metodi di punto interno).

Nell'ottimizzazione di problemi non lineari, dove il punto di minimo può di fatto cadere anche all'interno del dominio di ammissibilità, di fondamentale importanza è il concetto di convessità (sia del dominio sia della funzione obiettivo). Tra questi problemi rientra quello dei minimi quadrati, riconducibile anche a un sistema lineare di equazioni, per la risoluzione del quale esistono numerosi algoritmi ad hoc. Lo studio del caso generale, dal punto di vista sia teorico sia numerico, richiede ovviamente maggiore impegno. Le difficoltà più cruciali, nell'implementazione degli algoritmi iterativi per la minimizzazione, riguardano la scelta della direzione di discesa e l'entità del corrispondente passo.

Integrazione numerica e teoria dell'approssimazione

Uno dei settori dell'a. n. riguarda il calcolo dell'integrale definito ∫^b_a f  (x)dx di una funzione assegnata f. Escludendo il calcolo per via diretta attraverso una primitiva di f (raramente praticabile), è disponibile una moltitudine di algoritmi aventi caratteristiche differenziate. Essi nascono dall'idea di sostituire a f una funzione f_n che sia 'vicina' a essa quanto più possibile. A f_n viene richiesto di avere una rappresentazione elementare (lineare a tratti, polinomio a tratti, polinomio globale, polinomio trigonometrico, funzione spline ecc.). Per un dato n, l'algoritmo consiste nel calcolare esattamente ∫^b_a f _n (x)dx, mediante ben note regole elementari di integrazione. Più lo scarto fra f_n e f è basso e più ci si aspetta che ∫^b_a f _n (x)dx sia vicino al valore ∫^b_a f  (x)dx. Questo porta in generale allo studio delle successioni di funzioni f_n (al variare del parametro n) e della loro convergenza per n tendente a infinito, in una certa norma. Possiamo citare qualche metodo fra i più noti. Nel metodo del punto medio la funzione f viene approssimata da funzioni costanti a tratti, in quello dei trapezi da funzioni lineari a tratti e in quello di Cavalieri-Simpson da polinomi di secondo grado a tratti. Le formule di quadratura di tipo gaussiano sfruttano approssimazioni di f basate su polinomi globali di grado elevato. Tali polinomi interpolano f in opportuni nodi, quali quelli legati agli zeri dei polinomi ortogonali (Chebyshev, Legendre, Laguerre, Hermite ecc.).

L'esame approfondito di tecniche più sofisticate confluisce nei vasti capitoli della teoria dell'approssimazione e dell'analisi funzionale. In breve, individuato uno spazio di funzioni munito di una metrica, se ne considera un sottospazio di dimensione finita n. Data f nello spazio e scelta f_n come funzione 'approssimante' appartenente al sottospazio, si forniscono stime dell'errore f−f_n nella metrica assegnata. Molto spesso, quando possibile, f_n viene definita proprio come la funzione del sottospazio che minimizza la distanza da f. Altre volte f_n è la funzione interpolante f in punti assegnati. Occorre successivamente controllare che la differenza f−f_n tenda a zero per n tendente a infinito e stimare con quanta rapidità ciò avvenga.

Nella risoluzione numerica di gran parte delle equazioni funzionali (comprese quelle differenziali, v. oltre), l'algoritmo viene generato sostituendo il problema originale, avente per incognita f, con uno semplificato, molto simile, del quale una certa f_n è soluzione. Per es., è prassi rimpiazzare eventuali derivate, presenti nel problema iniziale, con rapporti incrementali e gli integrali con appropriate formule di quadratura. Si sfrutta poi il fatto che f_n è rappresentabile mediante un numero finito di gradi di libertà per costruire un sistema di equazioni (lineari o non lineari) che permettano il suo calcolo esplicito. Supposto di avere verificato le necessarie ipotesi, ci si aspetta che la differenza f−f_n sia effettivamente piccola, ricordando che quantitativamente ciò può venire valutato solo attraverso le stime dell'errore. La casistica dei problemi che possono essere affrontati in tale maniera è estremamente vasta, come pure le tecniche che si possono adottare. Un settore particolarmente sviluppato è, per es., quello delle equazioni integrali e delle equazioni differenziali con ritardo. Si restringe qui la trattazione ad alcuni esempi, quelli che storicamente possono essere ritenuti più significativi.

Equazioni differenziali ordinarie. - Il capitolo delle equazioni differenziali è di cruciale importanza per il mondo delle applicazioni. A tutti gli effetti, la nascita del calcolo infinitesimale è coincisa con la stesura dei primi modelli differenziali, espressamente finalizzati alla descrizione di fenomeni naturali. Nelle equazioni differenziali ordinarie ai valori iniziali, che descrivono l'evoluzione di sistemi dinamici in dimensione finita, l'incognita è una funzione y dipendente dalla variabile temporale t. A partire da un istante iniziale t=0, la funzione y evolve seguendo una legge del moto nella quale la y stessa e le sue derivate fino a un certo ordine si combinano. Per es., un tipico problema scalare del primo ordine prende la forma:

y'(t) = f (t, y(t)) k=1,2,3

anche se questa non è la scrittura più generale. La funzione f=f(t,y) viene assegnata, come pure il valore di y all'istante t=0. Tranne che per particolari scelte di f, non si dispone di tecniche di calcolo della soluzione esplicita y: è proprio per tale motivo che il ricorso a metodi numerici appare inevitabile. Come si è detto in precedenza, i metodi più spontanei nascono dalla sostituzione della derivata y' con formule alle differenze che equivalgono a rapporti incrementali. Per es., nel metodo di Eulero in avanti, assegnato il valore y₀=y(0), si costruiscono i successivi valori y_k mediante l'algoritmo:

Formula

  k=1,2,3,...

dove Δt>0 è un parametro assegnato e t_k=kΔt. Ci si aspetta allora che y_k− sia un'approssimazione di y all'istante t_k, a meno di un errore proporzionale a Δt (convergenza del primo ordine). Tutto ciò è vero, se le dovute ipotesi (che in questa sede non verranno menzionate) sono verificate. A partire da questa tecnica, molte altre sono state sviluppate successivamente. Fra queste, è uso distinguere fra metodi di tipo esplicito o implicito e fra metodi a un passo o a più passi (il metodo di Eulero in avanti è esplicito e a un passo). Nei metodi espliciti, il valore di y_k è immediatamente disponibile a partire dai valori calcolati in precedenza, mentre nei metodi impliciti y_k è ottenibile solo dopo aver risolto un'equazione non lineare. Un esempio di algoritmo implicito a un passo è dato dal metodo del punto medio:

Formula

  k=1,2,3,....

Detto metodo è più costoso del precedente, essendo necessario risolvere, a ogni passo k, un'equazione nell'incognita y_k. Tuttavia, esso porta a delle stime dell'errore dalle quali si deduce che la differenza y_k−y(t_k) si comporta come (Δt)² (convergenza quadratica oppure del secondo ordine).

Nei metodi a più passi, il valore di y_k, con k≥m, è deducibile (esplicitamente o implicitamente) non esclusivamente dal solo y_k−1, ma contemporaneamente dai valori y_k-1, y_k-2, y_k-3,…, y_k-m, dove m rappresenta il numero di passi. Per poter procedere con il calcolo è necessario assegnare opportunamente i valori iniziali y₀, y₁, y₂,…, y_m-1,.

Tra i metodi a disposizione per le equazioni differenziali ordinarie ne citiamo alcuni tra i più classici: Runge-Kutta, Adams-Bashforth, Adams-Moulton. A questi si aggiungono anche i metodi di tipo predictor-corrector. È difficile stabilire una graduatoria degli algoritmi a seconda delle prestazioni, essendo molti i parametri che entrano in gioco. Uno dei primi fattori da considerare è l'ordine di convergenza. I metodi impliciti sono in genere più onerosi di quelli espliciti, ma, se l'accuratezza non è una richiesta primaria, permettono di utilizzare dei valori di Δt non troppo piccoli, cosa che invece è spesso proibita ai metodi espliciti. I metodi a più passi (anche espliciti) hanno in genere un buon ordine di convergenza, ma richiedono l'utilizzo di maggiore memoria e la loro 'inizializzazione' è solitamente complicata. A monte di tutte queste considerazioni vi è il concetto di stabilità. A grandi linee, un metodo risulta essere stabile, per una scelta specifica di Δt, quando l'accumulo degli errori, dovuti al fatto di risolvere un problema approssimato a ogni iterazione, non è dominante. Al contrario, l'instabilità di un algoritmo porta a soluzioni numeriche il più delle volte non significative. Esistono varie definizioni di stabilità, principalmente legate al fatto di voler calcolare la soluzione numerica a un istante temporale fissato e con Δt tendente a zero, oppure che si voglia calcolare tale soluzione per tempi arbitrariamente lunghi, mantenendo Δt fisso. A un livello successivo di complessità troviamo i sistemi di equazioni differenziali ordinarie, di cui un esempio del primo ordine con due incognite y e z è dato da:

y'(t) = f (t, y(t)), z(t))

z'(t) = fg(t, y(t)), z(t))

dove le funzioni f e g sono assegnate insieme ai valori y(0) e z(0). A tali equazioni si possono applicare quasi tutti i metodi disponibili per il caso scalare. Utilizzando, per es., un metodo di tipo implicito, occorre risolvere a ogni passo un sistema di equazioni (lineare o non lineare, a seconda di come sono f e g), per il quale valgono le tecniche risolutive prese in considerazione precedentemente.

Equazioni alle derivate parziali. - Il capitolo relativo al trattamento numerico delle equazioni differenziali alle derivate parziali è sicuramente il più vasto, coinvolgendo tutte le tematiche sinora menzionate. La disciplina è estremamente vitale in quanto la maggior parte delle applicazioni (soprattutto in campo fisico e ingegneristico) è retta da modelli basati su equazioni alle derivate parziali, con dati iniziali e al contorno, spesso estremamente complessi. Rinunciando alla pretesa di essere esaustivi, si possono citare i problemi relativi alla meccanica delle strutture solide, sia sotto il profilo della statica sia della dinamica; i problemi di meccanica dei fluidi (quello delle previsioni meteorologiche è forse l'esempio più emblematico, anche se solo uno dei tanti); le equazioni della meccanica quantistica; i problemi legati ai fenomeni elettrici e della propagazione di onde elettromagnetiche in genere; le equazioni di Boltzmann. Più recenti sono le applicazioni in campo economico.

La tipologia delle equazioni è decisamente ampia. Nel caso lineare la classificazione consueta prevede la suddivisione in equazioni di tipo ellittico (determinazione di potenziali), di tipo parabolico (evoluzione con termini diffusivi) o di tipo iperbolico (evoluzione senza termini diffusivi), ma le equazioni (o i sistemi di equazioni) che si prospettano nella realtà vanno ben oltre questa casistica. Di volta in volta, la natura specifica della soluzione impone l'uso di tecniche numeriche alquanto differenziate, tanto che è impossibile fornire indicazioni generali di ogni sorta.

Ci si può pertanto limitare a qualche considerazione sommaria. Va tenuto conto che le difficoltà maggiori sono spesso legate, non tanto alla complessità delle equazioni, ma a quella della geometria dell'insieme su cui devono essere risolte. Tale geometria può addirittura variare con l'evoluzione temporale della soluzione, come per es. nei cosiddetti problemi di frontiera libera. Per equazioni nelle quali la parte ellittica è dominante prevalgono le tecniche numeriche di tipo variazionale. Il metodo degli elementi finiti è il più rappresentativo e ha da tempo inglobato e sostituito le più elementari tecniche alle differenze finite. Il dominio su cui sono definite le equazioni viene dapprima decomposto in un numero finito di triangoli o rettangoli (caso bidimensionale), tetraedri o parallelepipedi (caso tridimensionale). Su tali sottodomini semplificati vengono definiti gli 'elementi', che in genere vengono rappresentati da polinomi di grado prescelto (gli elementi lineari sono quelli che coinvolgono polinomi di primo grado).

La funzione approssimante viene quindi rappresentata attraverso un numero finito di gradi di libertà, dipendenti dal numero degli elementi e dal loro grado. Utilizzando tecniche di natura variazionale (per es. il metodo di Galerkin), si costruisce un sistema di equazioni, lineari o non lineari a seconda della natura dell'equazione differenziale. Il sistema viene poi risolto con uno degli algoritmi descritti in precedenza. L'ordine di convergenza è legato al grado degli elementi; quest'ultimo influisce anche sulla struttura del sistema di equazioni. In generale, una maggiore accuratezza corrisponde anche a un costo maggiore nella risoluzione, anche se le reali performances sono strettamente dipendenti dal comportamento della soluzione esatta. Nei problemi nei quali si ha anche una dipendenza dal tempo, si ricorre, per es., a una prima discretizzazione per quanto riguarda le variabili spaziali, riportandosi a un sistema di equazioni differenziali ordinarie, avente un numero di incognite che può essere molto grande. Successivamente, si adotta una delle tecniche, descritte brevemente in precedenza, e che sono disponibili per questo tipo di problemi.

Per quanto concerne il trattamento numerico di problemi di tipo iperbolico le difficoltà si inaspriscono ulteriormente. Le equazioni sono prevalentemente collegate a leggi fisiche di conservazione, le quali sono difficilmente riproducibili da parte della soluzione approssimante. Gli algoritmi appaiono sempre in bilico fra l'instabilità, che porta a dannose oscillazioni, e l'aggiunta di termini diffusivi (viscosità artificiale), che compromette la credibilità dell'approssimazione. A complicare le cose vi è il fatto che, durante l'evoluzione temporale, le soluzioni esatte possono degenerare in comportamenti discontinui (shock) o produrre, alla meno peggio, fronti d'onda con forte variazione. Nelle equazioni della fluidodinamica comprimibile, specialmente a regime supersonico, queste situazioni critiche sono riscontrate abitualmente.

Le ricerche più attuali nel campo della fluidodinamica computazionale riguardano la riproduzione di fenomeni di tipo caotico, quali quelli insiti nel regime di turbolenza di un fluido. Queste simulazioni, quando condotte su esempi che rispecchiano situazioni reali, richiedono ingenti tempi di calcolo su macchine di ottime prestazioni, anche ad architettura parallela. La sfida è quella di ideare algoritmi che permettano una drastica riduzione dei tempi di esecuzione, pur rimanendo affidabili. Si tenga infatti presente che una ragionevole accuratezza viene ottenuta grazie all'utilizzo di un grande numero di incognite, che i sistemi da risolvere sono spesso di natura non lineare, che a essi vanno abbinate tecniche per la discretizzazione nel tempo, che le geometrie sono complicate e possono evolversi con la soluzione. A ciò va aggiunto che il problema finale è spesse volte quello di ottimizzare certe parti (per es. il profilo alare di un velivolo), per cui la risoluzione numerica non si riferisce a una singola configurazione, ma va abbinata a metodi, del tipo dei minimi quadrati, per convergere alla configurazione più idonea.

Sempre nell'ambito delle equazioni alle derivate parziali, alcuni dei temi che hanno avuto notevole espansione negli ultimi anni riguardano le tecniche di decomposizione dei domini e gli algoritmi specificatamente ideati per calcolatori ad architettura parallela; il trattamento di equazioni con trasporto dominante; i metodi di ordine molto elevato (come per es. i p-metodi o metodi spettrali); lo studio del trattamento numerico di particolari condizioni al contorno; l'approssimazione di equazioni differenziali di tipo stocastico; l'ideazione di algoritmi adattivi.

Alcune nuove aree di ricerca hanno avuto un notevole sviluppo nell'ultimo decennio. Una gran parte delle applicazioni riguarda la ricostruzione di immagini digitali, settore che è attualmente molto in voga. A proposito segnaliamo l'analisi dell'approssimazione di fenomeni che si evolvono a più scale, che vedono in prima fila l'uso di funzioni approssimanti basate su wavelets. Nel campo della meccanica ha preso piede lo studio dei fluidi non newtoniani e dei mezzi granulari. Queste tematiche, anche privilegiate dalla crescente velocità di calcolo delle macchine e dal loro alto grado di parallelismo, hanno stimolato la nascita di originali e interessanti algoritmi.

bibliografia

K.E. Atkinson, An introduction to numerical analysis, New York 1966.

E. Isaacson, H.B. Keller, Analysis of numerical methods, New York 1966.

G. Dahlquist, Å. Björck, Numerical methods, Englewood Cliffs (NJ) 1974.

J. Stoer, R. Bulirsch, Introduction to numerical analysis, Heidelberg 1980.

Handbook of numerical analysis, ed. P.G. Ciarlet, J.L. Lions, Amsterdam-New York 1990.

Acta Numerica, Cambridge University Press, dal 1992.

W. Gautschi, Numerical analysis: an introduction, Basel 1997.