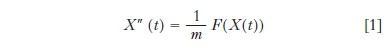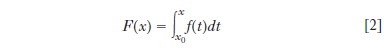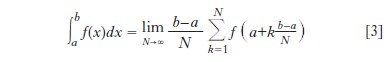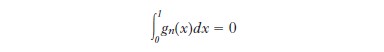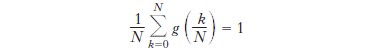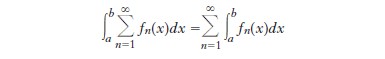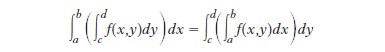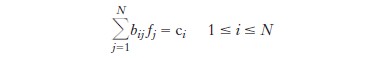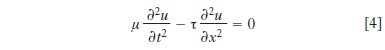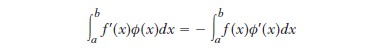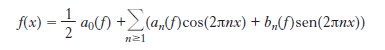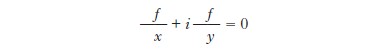ANALISI MATEMATICA

Analisi matematica

È molto difficile definire con precisione cos’è l’analisi matematica. Se si pensa all’algebra come al ramo della matematica consacrata al calcolo letterale e alle strutture nell’ambito delle quali tale calcolo ha senso, e se si pensa alla geometria come alla scienza delle figure, delle loro proprietà invarianti e dei modi di misurarle, si potrebbe pensare all’analisi come al ramo della matematica che studia il problema dell’approssimazione di quantità e la loro stabilità sotto l’effetto delle variazioni di questo o quel parametro da cui esse dipendono. Tuttavia, l’unità della matematica vieta di immaginare tali discipline come separate da frontiere ermetiche. Una tra le più importanti congetture della matematica, la congettura di Poincaré (di cui si parlerà più avanti), che verte su oggetti geometrici, non è stata risolta che nel 2006, da Grigorij J. Perelman, al termine di un programma definito nel 2002-03 e fondato su un approccio analitico sofisticato. D’altra parte, nulla potrebbe illustrare meglio i notevoli progressi ottenuti in fisica matematica negli ultimi dieci anni della celebre frase del fisico Eugene Wigner su «l’irragionevole efficacia della matematica nelle scienze naturali». Così, lo smorzamento di Landau, effetto di considerevole importanza in fisica dei plasmi scoperto da Lev D. Landau nel 1946, non è stato dimostrato rigorosamente come proprietà matematica delle soluzioni del sistema di equazioni di Vlasov-Poisson che nel 2010 da Clément Mouhot e Cédric Villani.

L’analisi matematica è dunque un tema immenso, del quale è impossibile dare una visione completa in poco spazio. Nel seguito si presenteranno, più modestamente, alcune delle idee fondamentali dell’analisi moderna, sviluppate intorno a un argomento centrale, lo studio delle equazioni differenziali, che gioca un ruolo eminente nei lavori appena elencati.

Calcolo differenziale e integrale

Fino all’inizio del 20° sec., l’analisi era il ramo della matematica consacrata allo studio delle funzioni di una o più variabili reali o complesse, e a valori reali o complessi. La meccanica, e in particolare l’astronomia, sono una fonte importante di problemi di analisi, dato che la seconda legge di Newton afferma che l’accelerazione di un punto materiale è proporzionale alla somma delle forze che si esercitano su di esso. In altre parole

indicando con m la massa del punto, con X(t) la sua posizione all’istante t e con X″ la sua derivata seconda rispetto alla variabile t, e con F(X) la forza esercitata su tale punto quando esso si trova nella posizione X. Questo è un esempio di equazione differenziale, nella quale la funzione X è l’incognita cercata, mentre il campo di forza F e la massa m sono dati. Predire il moto dei pianeti, o dei loro satelliti, si riconduce dunque a risolvere sistemi di equazioni differenziali analoghe alla [1], dove il campo di forze F è assegnato dalla legge di gravitazione universale di Newton.

Trattare questi problemi richiede un quadro rigoroso per il calcolo differenziale e integrale. Si ricorda che la derivata in x0 di una funzione numerica f della variabile x definita nell’intorno di x0 è il limite del rapporto incrementale (f(x0+h)−f(x0))/h quando h tende a zero, limite indicato con f′(x0), quando questo esiste. Questo limite definisce una nuova funzione, indicata con f′, che si può derivare dove è possibile, definendo così la derivata seconda f″ di f. Si definiscono, per ricorrenza, le derivate successive di f, e si indica con f(k) la derivata k-ma di f. Geometricamente, f′(x0) è la pendenza della tangente alla curva d’equazione y=f(x) nel punto (x0, f(x0)). Se x(t) è la posizione di un punto all’istante t, la derivata x′(t) è la sua velocità e la sua derivata seconda x″(t) la sua accelerazione all’istante t. Inversamente, data una funzione f, si cercano le funzioni F tali che F′=f, dette primitive di f. Due primitive di f differiscono per una costante, e si indica con

la primitiva di f tale che F(x0)=0, che viene chiamata integrale di f da x0 a x. Geometricamente, l’integrale di f da a a b è l’area delimitata dall’asse delle ascisse, le rette di equazioni x=a e x=b, e la curva d’equazione y=f(x), in modo tale che

Questa rappresentazione è sufficiente quando f è data da una formula che compone funzioni di uso comune (polinomi, esponenziali, logaritmi, funzioni trigonometriche ecc.), a condizione di evitare punti singolari eccezionali. Le soluzioni di alcune equazioni differenziali, quali [1] nel caso di un pianeta sottoposto alla sola attrazione gravitazionale del Sole, sono di questo tipo, e le formule esatte che danno queste soluzioni si ottengono attraverso vari procedimenti fondati sul calcolo differenziale e integrale descritto precedentemente. Ma, se n>2, il moto di punti materiali sottoposti alla propria mutua attrazione gravitazionale non può essere ottenuto nella stessa maniera in tutta generalità (Henri Poincaré, 1889). D’altra parte, le equazioni differenziali che si sanno risolvere esattamente per mezzo delle funzioni classiche evocate sopra sono l’eccezione, piuttosto che la regola. In mancanza di formule esatte che esprimano le soluzioni di equazioni differenziali generali a partire da un piccolo numero di funzioni note e tabulate con precisione arbitraria, bisogna cercare metodi sistematici per ottenerne valori approssimati.

Ora, le nozioni di derivata e integrale definite precedentemente mal si combinano con la convergenza di successioni di funzioni. Per es., la successione di funzioni (per ogni reale x, si designa con [x] la sua parte intera, cioè il più grande intero ≤x) fn(x)=2−nmin(2nx−[2nx],1−2nx +[2nx]) della variabile reale x converge a 0 uniformemente in x quando n→∞, dal momento che 0≤fn(x)≤2−n; tuttavia f′ n(x)=±1 per x≠k/2n, con k intero. Allo stesso modo, sia gn la successione di funzioni della variabile reale x tali che gn(p/q)=1 per p, q interi tali che 0≤p≤q≤n e gn(x)=0, se x non è di tale forma. La successione gn, crescente in n, converge alla funzione g tale che g(x)=1 se x è un numero razionale dell’intervallo [0,1] e g(x)=0, altrimenti, sebbene

mentre

Henri Lebesgue costruì nel 1902 una nozione di integrale coincidente con quella definita da [2] e [3] quando f è continua, ma per la quale

per ogni successione fn di funzioni integrabili a valori positivi (Beppo Levi, 1906). La costruzione di Lebesgue si estende alle funzioni di più variabili; Guido Fubini (1907) e Leonida Tonelli (1909) hanno precisato sotto quali condizioni per una funzione f di due variabili x e y si ha

Nella teoria di Lebesgue, l’integrazione non è più in generale l’operazione inversa della derivazione, restando vera la formula F′=f, dove F è data dalla formula [2] se f è continua. Altri autori (Oskar Perron, Arnaud Denjoy, Ralph Henstock, Jaroslav Kurzweil) hanno costruito nozioni d’integrali che corrispondono esattamente all’inverso della derivazione. Tuttavia in queste teorie, al contrario di quella di Lebesgue, può verificarsi che una funzione f non sia integrabile malgrado lo sia il suo valore assoluto |f|.

Analisi funzionale

La teoria di Lebesgue dell’integrazione apre la strada all’analisi funzionale, nella quale le funzioni divengono punti di uno spazio vettoriale di dimensione infinita (i valori f(t) assunti da f per t reale essendo gli analoghi delle coordinate (x1,..., xn) di un punto dello spazio a n dimensioni). La ‘distanza’ tra due funzioni f e g è data dall’espressione analoga a quella che dà la distanza tra due punti di uno spazio euclideo di dimensione finita. Le applicazioni di questa prospettiva sono numerose.

Essa ha permesso a Erik Fredholm, David Hilbert e Vito Volterra di elaborare, al principio del 20° sec., una teoria delle equazioni integrali, della forma

in cui a, b, c sono funzioni assegnate, mentre f è l’incognita, in analogia con la teoria dei sistemi di equazioni lineari di N equazioni in N incognite, della forma

dove i numeri b_ij e c_i sono dati, mentre le incognite sono i numeri f₁,..., f_n. Successivamente, a partire dagli anni Trenta e dai lavori di Werner K. Heisenberg e di Erwin Schrödinger, l’analisi funzionale è diventata l’ambito geometrico della meccanica quantistica (John von Neumann, Mathematische Grundlagen der Quantenmechanik, 1932). A partire dagli anni Ottanta, questo quadro è evoluto, sotto l’impulso di Alain Connes, verso la geometria non commutativa, nella quale la nozione di punto non gioca più un ruolo fondamentale, e dove la moltiplicazione degli oggetti analoghi alle coordinate dei punti nel quadro classico dipende in generale dall’ordine dei fattori, cosa che generalizza in qualche modo il principio d’indeterminazione di Heisenberg.

Distribuzioni ed equazioni alle derivate parziali

A partire dal 18° sec., i progressi della fisica diedero vita a equazioni differenziali più complesse di [1], nelle quali la funzione incognita dipende da più variabili reali: tali equazioni differenziali sono dette equazioni alle derivate parziali (EDP). Uno dei primi esempi ne è l’equazione della corda vibrante (Jean-Baptiste d’Alembert, 1747). Data una funzione f=f(x,y) di due variabili reali, si indica con ∂f/∂x la derivata di f vista come funzione della variabile x quando y resta costante, la notazione ∂f/∂y designando la derivata ottenuta scambiando i ruoli di x e y. Queste operazioni possono essere reiterate: ∂²f/∂x² è la funzione ∂/∂x(∂f/∂x), mentre ∂²f/∂x∂y=∂/∂x(∂f/∂y) e così via. Così, l’equazione della corda vibrante, detta anche equazione delle onde, di incognita u=u(t,x), che rappresenta lo spostamento della corda nel punto x all’istante t, si scrive

dove μ è la massa lineare della corda e τ la sua tensione. La soluzione generale di tale equazione è u(t,x)=a(x−ct)+b(x+ct), dove a e b sono funzioni arbitrarie di una sola variabile, e in cui c=(τ/μ)^1/2. Questa formula descrive la propagazione di due onde che si muovono con velocità c lungo la corda e in direzioni opposte. Essa conserva evidentemente lo stesso significato fisico anche quando a e b non sono derivabili, cioè quando il limite che interviene nella definizione usuale della derivata non esiste per a o b o per le loro derivate. Il fenomeno delle onde d’urto in dinamica dei gas fornisce un altro esempio di soluzioni di un sistema di EDP (introdotto da Eulero nel 1755) per le quali la definizione usuale è insufficiente. Si cercò dunque di generalizzare la nozione di derivata, e si giunse tra il 1930 e il 1950, sotto l’impulso delle idee di Sergej Sobolev, Jean Leray e soprattutto Laurent Schwartz, a una teoria soddisfacente, nella quale le funzioni sono immerse in una classe più vasta di oggetti, le distribuzioni. L’idea chiave consiste nel partire dalla formula d’integrazione per parti: date due funzioni f=f(x) e φ=φ(x) regolari, che possono essere derivate in ogni punto usando la formula abituale, si ha

quando φ è nulla sul bordo dell’intervallo [a,b]. L’idea è di definire la ‘derivata’ di f tramite il membro di destra dell’uguaglianza data sopra quando non si può utilizzare la definizione data dal procedimento abituale. Da questo nuovo punto di vista, la nozione di funzione si generalizza in quella di distribuzione. Le distribuzioni sono funzionali lineari sullo spazio delle funzioni infinitamente derivabili e nulle vicino al bordo del loro dominio di definizione. La massa di Dirac in un punto x₀ della retta reale, indicata con δ_x0, è l’esempio più semplice di distribuzione che non sia una funzione: il valore da essa assunto su una funzione infinitamente derivabile sulla retta reale è (δ_x0, φ)=φ(x₀). La sua derivata è la distribuzione indicata con δ′_x0, definita dalla formula (δ′_x0, φ)=−φ′(x₀). Dire che la funzione u è soluzione dell’equazione [4], nel senso delle distribuzioni, corrisponde a moltiplicare ogni membro della [4] per una funzione arbitraria infinitamente derivabile φ nulla nell’intorno dell’infinito, poi a integrare per parti nelle diverse variabili, per fare insistere tutte le derivate su φ (ciò è l’analogo del principio dei lavori virtuali, risalente a Johann Bernoulli, d’Alembert, Eulero e Joseph-L. Lagrange, e che è alla base della meccanica analitica e del calcolo delle variazioni).

Il contesto delle distribuzioni fornisce allora una soluzione completa di tutte le EDP lineari a coefficienti costanti. In elettrostatica, si sa che il potenziale V(x,y,z) creato nel punto di coordinate (x,y,z) da una distribuzione di cariche ρ≡ρ(x,y,z) verifica da un lato l’equazione di Poisson −ΔV=ρ, dove si è indicato con Δ=∂²/∂x²+∂²/∂y²+∂²/∂z²,e dall’altro che è la sovrapposizione dei potenziali coulombiani creati in ciascun punto dalla distribuzione di cariche ρ. Ora, il calcolo delle distribuzioni mostra che il potenziale coulombiano creato da una carica +1 nell’origine, cioè G(x,y,z)=(1/4π)(x²+y²+z²)^−1/2, verifica −ΔG=δ₀. Le soluzioni generali, nel senso delle distribuzioni, dell’equazione di Poisson −ΔV=ρ, si ottengono come sovrapposizioni pesate di funzioni traslate della funzione G. Questa idea si generalizza a ogni EDP lineare a coefficienti costanti. Dato un operatore differenziale P a coefficienti costanti, è sufficiente dunque trovare una distribuzione E tale che PE=δ₀, detta soluzione fondamentale di P. La soluzione generale si ottiene per sovrapposizione di traslate di E, come nel caso dell’equazione di Poisson. Dato che Leon Ehrenpreis e Bernard Malgrange hanno dimostrato indipendentemente (1954-56) che ogni operatore differenziale lineare a coefficienti costanti ammette una soluzione elementare, il metodo accennato sopra riconduce lo studio delle soluzioni di EDP della forma Pu=ρ di incognita u, dove ρ è una distribuzione data, a quello delle proprietà di E.

Il caso delle EDP lineari a coefficienti variabili, ma regolari (infinitamente derivabili) è più complicato, e rende necessario sviluppare strumenti più sofisticati dell’analisi armonica, come gli operatori pseudodifferenziali o integrali di Fourier (seguendo Joseph John Kohn, Louis Nirenberg, Peter Lax, Lars Hörmander), cosa che fu fatta tra il 1955 e il 1975. È illusorio sperare di avere in questo caso formule esplicite di rappresentazione delle soluzioni, come nel caso dell’equazione delle onde, ma si può sperare di descrivere le ‘singolarità’ delle soluzioni, cioè i punti vicino ai quali le distribuzioni che sono soluzioni non coincidono con una funzione infinitamente derivabile. Questo punto di vista, che risale alla nozione di parametrice (cioè di soluzione ‘modulo errori eventualmente grandi ma regolari’) fu sistematicamente esplorato negli anni Settanta da Lars Hörmander e dalla sua scuola. La nozione centrale di questa branca dell’analisi, detta microlocale, è quella di ‘fronte d’onda’, in analogia con la teoria di Huygens dell’ottica geometrica. La propagazione delle onde luminose è retta dalle equazioni di Maxwell, trattandosi di onde elettromagnetiche. Quando la lunghezza d’onda è piccola rispetto agli oggetti illuminati, le soluzioni tendono a propagarsi come curve ortogonali alle superfici d’onda, e i raggi luminosi corrispondono alle singularità delle soluzioni delle equazioni di Maxwell. Questa analogia fu messa a frutto in modo sistematico tra il 1960 e il 1980 nei lavori di Joseph B. Keller, Viktor Pavlovic Maslov, Leray e Hörmander.

Ma evidentemente, le poche idee accennate sopra non permettono in generale di affrontare le EDP non lineari (cioè quelle per le quali una sovrapposizione di soluzioni non è più necessariamente soluzione). L’analisi non lineare è un ramo particolarmente attivo della matematica della fine del 20° e dell’inizio del 21° secolo. La nozione di distribuzione è poco adatta all’analisi non lineare: non è possibile in generale moltiplicare le distribuzioni (per es., non si sa dare significato a δ₀² nel contesto delle distribuzioni). D’altra parte, la nozione di soluzione nel senso delle distribuzioni può portare, per le EDP non lineari, a strani paradossi: per es., esistono soluzioni di EDP proposte da Eulero per descrivere la meccanica dei fluidi incompressibili non viscosi che corrispondono a situazioni nelle quali un fluido, inizialmente a riposo, si mette in moto senza azione di forze esterne, poi torna a riposo dopo un tempo finito (Vladimir Scheffer, 1993; Alexander Schnirelman, 1997; Camillo De Lellis-László Szekelyhidi, 2009). Per quanto riguarda il moto dei fluidi viscosi incompressibili nello spazio, Leray ha costruito, a partire dal 1934, soluzioni nel senso delle distribuzioni definite per tutti i tempi per ogni dato iniziale di energia finita. Si ignora attualmente se tali soluzioni possano sviluppare singolarità in tempo finito; si sa solamente che le singolarità eventuali sono molto rare, dato che riempiono al massimo una curva nello spazio-tempo (Luis Caffarelli, Robert V. Kohn, Louis Nirenberg, 1984). Malgrado tali difficoltà, alcune idee provenienti dall’analisi delle EDP non lineari hanno svolto un ruolo importante in altre branche della matematica. La celebre congettura di Poincaré (1904) affermava che l’ipersfera di dimensione 3 potesse essere caratterizzata da alcune proprietà topologiche (ogni varietà compatta senza bordo e semplicemente connessa è omeomorfa a una ipersfera di dimensione 3). La dimostrazione di questa congettura – effettuata da Perelman nel 2003 – comporta l’uso di un sistema di EDP non lineari, le equazioni del ‘flusso di Ricci’ (Richard Hamilton, 1982); una delle idee chiave di Perelman è stata quella di considerare una quantità che, per tali equazioni, gioca un ruolo analogo a quello dell’entropia per l’equazione del calore.

Evento di grande rilevanza del 20° sec. nella teoria delle EDP è la possibilità di calcolarne numericamente le soluzioni tramite elaboratori. I primi calcolatori elettronici (ENIAC, Electronic Numerical Integrator And Computer, 1946) hanno fatto capire l’interesse dello studio sistematico della convergenza dei metodi di soluzione numerici per le EDP. I primi risultati matematici in questa direzione furono ottenuti da John von Neumann, Peter Lax, Robert Richtmyer verso la fine degli anni Quaranta. L’analisi numerica si sviluppò rapidamente a partire da tale epoca, per diventare una delle branche più importanti della matematica.

Analisi armonica

Nel 1822, Jean Baptiste Fourier propose una teoria della propagazione del calore nei solidi; egli giunse all’equazione ∂T/∂t=κ∂²T/∂x², nella quale l’incognita T=T(t,x) è la temperatura nel punto x all’istante t e dove κ è un reale positivo. Cercando soluzioni della forma T=T(t,x)=g(t)f(x), egli fu indotto a proporre di scomporre ogni funzione periodica (per es., di periodo 1) sotto forma di una sovrapposizione finita di funzioni trigonometriche:

Il significato da dare a una tale uguaglianza, e la sua validità in funzione della regolarità della funzione f, costituirono l’obiettivo dei più grandi matematici nel 19° e nel 20° secolo. Dopo i lavori di Johann Peter Gustav Dirichlet, Camille Jordan, Jacques Hadamard, Lipót Fejer, Ulisse Dini, Nikolai Nikolaevic Lusin, Andrei Nikolaevic Kolmogorov e altri, Lennart Carleson dimostrò nel 1966 che questa uguaglianza vale per ogni funzione a quadrato sommabile e per quasi ogni x (cioè al di fuori di un insieme che può essere ricoperto da una successione di intervalli la cui somma delle lunghezze è arbitrariamente piccola). Questa rappresentazione delle funzioni periodiche venne in seguito estesa a varie classi di funzioni non periodiche sulla retta reale, poi al contesto delle distribuzioni da Laurent Schwartz, così come a gruppi più generali della retta reale dotata di addizione. Essa gioca un ruolo considerabile nello studio delle equazioni differenziali, perché, per es., i coefficienti di f″ sono ottenuti a partire da quelli di f attraverso le seguenti semplici formule: a_n(f ″)=−(2πn)²a_n(f) e b_n(f ″)= −(2πn)²b_n(f). L’idea di scomporre ogni funzione come sovrapposizione di un sistema di funzioni particolari, molto adatte all’osservazione di questa o quella proprietà matematica, è stata oggetto di numerose ricerche negli anni Ottanta del secolo scorso: ne è un esempio la teoria dellewavelets, che permette di localizzare al meglio in spazio (nella variabile x) e frequenza (cioè in n), sviluppata da Alexander Grossman, Yves Meyer e Jean Morlet, successivamente da Stéphane Mallat e Ingrid Daubechies, e che interviene negli algoritmi di compressione d’immagine (JPEG2000).

Analisi complessa

L’analisi delle funzioni f=f(z) a valori complessi di una variabile complessa z derivabili nel senso che il loro tasso di crescita ammette un limite (complesso) in ogni punto, dette funzioni olomorfe, fa ugualmente intervenire una EDP particolare. Indicando con x=Rez e con y=Imz rispettivamente la parte reale e immaginaria di z, si trova che le funzioni olomorfe sono soluzioni dell’EDP Formula.

Le funzioni olomorfe hanno proprietà di ‘rigidità’ notevoli. Per es., una funzione olomorfa su un disco aperto del piano complesso è completamente determinata dall’assegnazione del suo germe in un solo punto del disco, cioè dalla successione delle sue derivate successive in tale punto. Ciò è falso per una funzione infinitamente derivabile di una variabile reale, come mostra l’esempio della funzione definita come f(x)=e^1/x per x<0 e f(x)=0 per x≥0; questa funzione è non identicamente nulla, benché f(0)=f′0)= f″(0)= ... =0. Le funzioni olomorfe intervengono in una grande varietà di contesti: in fisica (descrizione del moto piano di fluidi incompressibili non viscosi e senza vorticità), in geometria (trasformazioni conformi, cioè che conservano gli angoli, del piano), o ancora in teoria dei numeri. Per es., Bernhard Riemann mostrò nel 1859 che lo studio della funzione ζ(s)=1+1/2^s+1/3^s+ ... +1/n^s+..., prolungata in una funzione olomorfa nel piano complesso privato del punto s=1 – più precisamente dei valori di s per i quali ζ(s)=0 –, fornisce informazioni sulla distribuzione dei numeri primi. Se si indica con π(x) il numero di numeri primi ≤x, il teorema dei numeri primi afferma che π(x)ln(x)/x→1 quando x→∞. Questo enunciato, congetturato da Carl F. Gauss, è stato infine dimostrato (indipendentemente) da Jacques Hadamard e Charles Jean de la Vallée Poussin nel 1896, come conseguenza del fatto che ζ(s)≠0 quando Re(s)=1. L’ipotesi di Riemann, vale a dire che ζ(s)≠0 quando Re(s)>1/2, fornirebbe una stima del termine di errore asintotico nel teorema dei numeri primi. Tale questione, rimasta aperta ancora oggi, è una delle più misteriose di tutta la matematica.

Più recentemente, la dinamica olomorfa, inaugurata ver so il 1918 da Pierre Fatou e Gaston Julia, che si erano interessati alle iterazioni di trasformazioni del piano complesso definite da polinomi o da frazioni razionali, poi da Carl L. Siegel (1942), che aveva studiato la possibilità di ricondurre la dinamica delle iterazioni di una trasformazione olomorfa in prossimità di un punto fisso a quella della sua parte lineare, ha conosciuto una ripresa di attività, in particolare grazie alla possibilità di realizzare esperienze numeriche su microcalcolatori. Sono comparsi nuovi oggetti legati alla dinamica (insiemi di Mandelbrot, ‘coniglio di Douady’ ecc.), e queste idee intervengono nella soluzione completa ottenuta da Jean-C. Yoccoz (1995) del problema studiato da Siegel.

Bibliografia

V.I. Arnold, Ordinary differential equations, Cambridge (Mass.) 1973; L.V. Ahlfors, Complex analysis, New York 19793; W. Rudin, Real and complex analysis, Singapore 19863; V.I. Arnold, Geometrical methods in the theory of ordinary differential equations, New York 19882; V.I. Arnold, Mathematical methods of classical mechanics, New York 19892; P. Malliavin, H. Airault, G. Letac, L. Kay, Integration and probability, New York 1995; P.D. Lax, Functional analysis, New York 2002; Y. Katznelson, An introduction to harmonic analysis, Cambridge 20043; T. Tao, Poincaré legacies: pages from year two of a mathem atical blog, 1° e 2° voll., Providence (R.I.) 2009; L.C. Evans, Partial differential equations, Providence (RI) 20102; T. Tao, An epsilon of room: pages from year three of a mathematical blog, 1° e 2° voll., Providence (R.I.) 2010, 2011; C. Mouhot, C. Villani, On Landau damping, «Acta mathematica», 2011, 207, pp. 29-201.

Webgrafia

G. Perelman, The entropy formula for the Ricci flow and its geometric applications, 2002, http://arxiv.org/pdf/ math/0211159 v1.pdf; G. Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds, 2003, https://arxiv.org/pdf/%20math/%200307245v1.pdf; G. Perelman, Ricci flow with surgery on three-manifolds, 2003, http://arxiv.org/ pdf/math/0303109v1.pdf.