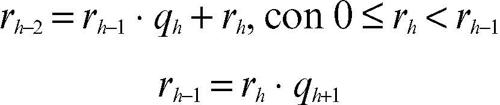Euclide, algoritmo di
Euclide, algoritmo di
Euclide, algoritmo di (per il MCD) o algoritmo delle divisioni successive, algoritmo che, dati due numeri interi a e b, permette di calcolarne il → massimo comune divisore mcd(a, b). Esso si fonda su una successione finita di divisioni con resto, in modo che il divisore e il resto (qualora non nullo) di una divisione diventino rispettivamente il dividendo e il divisore della divisione successiva. L’algoritmo ha termine quando si trova un resto nullo: l’ultimo resto diverso da zero fornisce la soluzione del problema. Si può supporre che a e b siano entrambi positivi con a maggiore di b: se così non fosse, infatti, si potrebbe scambiarli eventualmente con il loro opposto e permutarli tra loro e tali operazioni non altererebbero il loro massimo comun divisore. Al primo passo, si divide a per b e, se q1 e r1 indicano rispettivamente il quoziente e il resto di tale divisione, si ottiene
Se r1 = 0, allora l’algoritmo ha termine e fornisce la soluzione mcd(a, b) = b; altrimenti si procede con la divisione successiva, ottenuta dividendo b per r1:
Se r2 = 0, allora l’algoritmo ha termine e fornisce la soluzione mcd(a, b) = r1; altrimenti si procede in modo analogo con le divisioni successive fintanto che si ottiene un resto rh positivo tale che il resto successivo è zero. Pertanto gli ultimi due passi saranno
A questo punto l’algoritmo ha termine e fornisce la soluzione mcd(a, b) = rh.
Formalizzando le successive operazioni in linguaggio algoritmico (per poi eventualmente codificarle in un linguaggio di programmazione), si può così rappresentare l’algoritmo (in cui «mod» indica il resto della divisione intera):
Per esempio, per trovare mcd(120, 264), l’algoritmo procede nel modo seguente:
mcd(120, 264) = mcd(264, 120)
b > 0 vero
r = mod(264, 120) = 24
a = 120
b = 24
b > 0 vero
r = mod(120, 24) =0
a = 24
b = 0
b > 0 falso
24 è il mcd cercato
L’algoritmo di Euclide può essere riformulato in modo sostanzialmente analogo nel caso di due polinomi a coefficienti reali in una indeterminata, purché si sostituisca a ogni passo la condizione 0 ≤ ri < ri−1 con la condizione
dove ri (x) è l’i-esimo resto ottenuto e «deg» indica il grado del polinomio. Più in generale, l’algoritmo di Euclide può essere riformulato in ogni dominio euclideo D, richiedendo a ogni passo che sia verificata la condizione
dove ν: D − {0} → N è la valutazione definita in D.