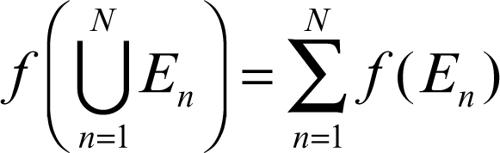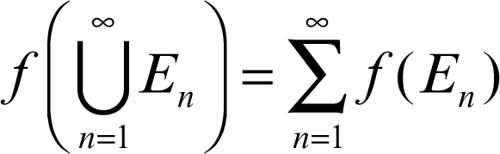additività

additivita

additività in termini generali, proprietà di una funzione ƒ, definita in uno spazio vettoriale V, espressa dall’uguaglianza ƒ(x + y) = ƒ(x) + ƒ(y) e valida per ogni x, y in V. Nel suo significato più elementare, il termine additività indica in sostanza la proprietà di una funzione di preservare l’operazione di addizione per ogni coppia di elementi per cui essa è definita. In altre aree della matematica, il termine assume significati meno immediati.

☐ In teoria dei numeri, si parla di additività di una funzione aritmetica per indicare la proprietà espressa dall’uguaglianza ƒ(x + y) = ƒ(x) + ƒ(y), essendo x e y due numeri primi tra loro (o coprimi). Se tale uguaglianza vale per tutte le coppie di numeri interi positivi (anche non primi tra loro) si parla di additività completa. Una funzione completamente additiva è additiva, ma non viceversa. La funzione logaritmo, definita in N, è un esempio di funzione completamente additiva.

☐ In teoria della misura, una funzione d’insieme ƒ(E), definita su una σ-algebra, si dice (finitamente) additiva se per ogni famiglia finita {E_n} di insiemi a due a due disgiunti risulta

Si parla di additività numerabile se tale proprietà si estende a famiglie numerabili di insiemi disgiunti e si ha l’uguaglianza:

La funzione d’insieme in tal caso è detta numerabilmente additiva.