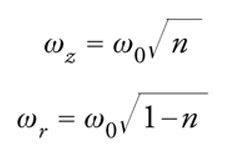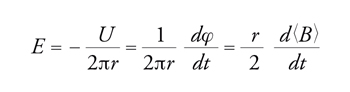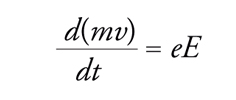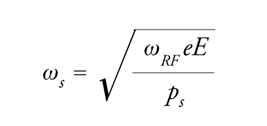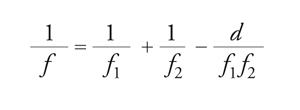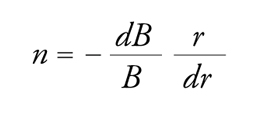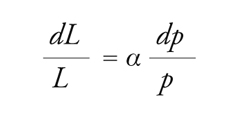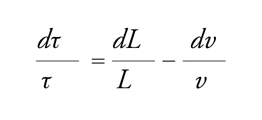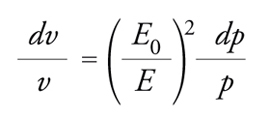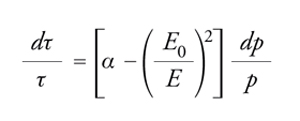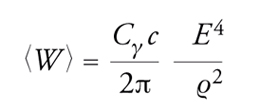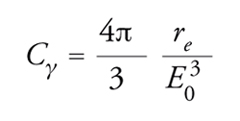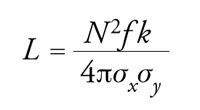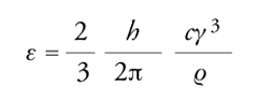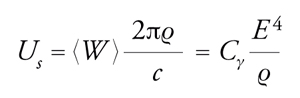Acceleratori circolari di particelle
Acceleratori circolari di particelle
Gli acceleratori di particelle permettono di indagare le leggi fondamentali della natura facendo collidere particelle accelerate con altre ferme o in movimento e trasformando energia cinetica in materia secondo la relazione E=mc2. I primi acceleratori furono costruiti sul finire degli anni Venti del secolo scorso e rapidamente divennero il principale e più perfezionato strumento di indagine nella fisica delle alte energie. A distanza di oltre otto decenni, soltanto un'esigua minoranza dei circa quindicimila acceleratori operanti nel mondo è destinata alla ricerca fondamentale, mentre la maggior parte trova impiego in fisica applicata (nello studio della struttura della materia, delle proprietà dei solidi e delle superfici, nella caratterizzazione di cristalli), in biologia e medicina (per scopi terapeutici e diagnostici) e in campo industriale (nello studio dell'integrità di solidi complessi, nelle ispezioni a distanza, nella sterilizzazione di alimenti). Le macchine acceleratrici possono avere una struttura lineare oppure ciclica e generalmente impiegano elettroni, protoni o nuclei completamente ionizzati. In origine, gli acceleratori adoperavano campi elettrostatici prodotti da due elettrodi ad alta tensione, posti in una struttura lineare in cui era stato praticato il vuoto. La difficoltà di operare con un campo elettrico sempre più elevato suggerì di utilizzare accelerazioni elettrostatiche multiple o di ricorrere all'induzione elettromagnetica. Rolf Wideröe usò fin dal 1928 una serie di elettrodi cilindrici di lunghezza crescente, ai quali era applicata una tensione rapidamente variabile, detta tensione a radiofrequenza o tensione RF, tale che le particelle incontravano, nel passaggio da un elettrodo al successivo, un campo accelerante.
Nel 1931 David H. Sloan ed Ernest O. Lawrence misero a punto un acceleratore lineare dotato di trenta elettrodi, in grado di conferire a ioni di mercurio un'energia di 1,26 MeV. Negli anni Trenta, la corsa a energie sempre più elevate portò all'invenzione del ciclotrone, una macchina circolare a focalizzazione debole. Il principio di funzionamento fu proposto simultaneamente da diversi fisici, tra cui Jean Thibaud, Leo Szilard e lo stesso Lawrence, ma trovò applicazione per opera esclusivamente di quest'ultimo e dei suoi collaboratori a Berkeley: le particelle cariche, protoni o nuclei ionizzati, percorrevano orbite spiraleggianti per effetto combinato di un campo magnetico e di una tensione RF applicata a due elettrodi a forma di cavità emicilindriche; il fatto che l'accelerazione avvenisse con frequenza fissa rendeva però impossibile raggiungere energie relativistiche. Il betatrone, un acceleratore per elettroni costruito da Donald William Kerst nel 1940, si basava sull'induzione magnetica e rappresentò un passo cardinale verso il raggiungimento di energie ultrarelativistiche. Queste furono ottenute mediante il sincrotrone, in cui la frequenza del campo accelerante era adattata continuamente alla velocità di rivoluzione delle particelle. Il cammino verso la costruzione di sincrotroni compatti ed economici fu reso possibile dal principio di 'stabilità di fase' e da quello di 'gradiente alternato', o di focalizzazione forte. Negli anni Sessanta furono inventati gli anelli di collisione (grazie a Bruno Touschek e Gerard K. O'Neill), nei quali due fasci di particelle, ruotando in direzioni opposte, possono scontrarsi l'uno contro l'altro.
sommario:
1. Gli accelatori circolari. 2. Il principio di stabilità di fase e sue applicazioni. 3. Il principio della focalizzazione forte dovuto a gradienti alternati. 4. Sincrotroni a gradiente alternato per elettroni: il caso del LEP. 5. Breve storia degli anelli di collisione. 6. Anelli di collisione per protoni: il caso LHC.
Gli acceleratori circolari
Il ciclotrone
Il ciclotrone è un acceleratore circolare per protoni e nuclei leggeri, che trova largo impiego in fisica nucleare e per applicazioni mediche. I suoi componenti essenziali sono un magnete con poli circolari, che genera un campo costante, e due elettrodi cavi affiancati, di forma emicilindrica, alimentati con una tensione a radiofrequenza fissa la cui proiezione nel piano orizzontale ricorda la lettera 'D' (da cui il nome dees in inglese). Una particella di carica e, che si muova con velocità v in presenza di un campo magnetico B costante, è soggetta alla forza di Lorentz F=ev×B, centripeta, ortogonale sia al campo sia alla velocità della particella e tale da non modificare né l'energia cinetica né la componente del moto nella direzione di B. Se il campo magnetico è costante e uniforme, e la velocità iniziale è a esso ortogonale, il moto è circolare uniforme. Dalla formula per la forza centripeta si ottiene la relazione evB=mv2/r tra la componente della velocità ortogonale al campo, la massa della particella e il raggio della traiettoria. La velocità angolare e l'energia cinetica valgono rispettivamente:
[1] ω = v/r = eB/m
[2] Ecin = 1/2 mv2 = 1/2 e222/m.
Nel ciclotrone, per effetto del campo magnetico, le particelle percorrono all'interno di ciascun elettrodo traiettorie semicircolari. Nel passaggio fra un elettrodo e l'altro ricevono un impulso dalla tensione RF e, qualora la radiofrequenza sia sincrona con quella [1] di rivoluzione, l'accelerazione impartita è risonante. La sorgente delle particelle è posta nel centro del ciclotrone: la velocità angolare di rivoluzione si conserva costante, ma a ogni attraversamento degli elettrodi aumentano il raggio della traiettoria e la velocità delle particelle, che dopo un centinaio di giri, seguendo un tragitto simile a una spirale, si portano dal centro alla periferia del magnete. L'energia cinetica finale è data dalla formula [2], ove s'interpreti r come il raggio del magnete. In un ciclotrone, però, è impossibile raggiungere energie relativistiche, che implicherebbero un aumento della massa e di conseguenza una diminuzione della frequenza di rivoluzione, tale da pregiudicare il sincronismo con la tensione RF e ostacolare l'ulteriore incremento di energia: il valore limite è circa di 15 MeV per i protoni, di 50 MeV per i deuteroni e per le particelle α e di soli 2 MeV per gli elettroni, per i quali i ciclotroni risultano del tutto inadeguati. I più potenti, in ogni caso, sono oggi dotati di magneti superconduttori e di sistemi che, opportunamente sincronizzati, permettono di accelerare i protoni fino a energie di alcune centinaia di MeV.
Stabilità delle orbite
In un ciclotrone immerso in un campo magnetico rigorosamente uniforme, particelle dotate di una componente del moto parallela al campo stesso percorrerebbero traiettorie elicoidali e sarebbero sospinte inevitabilmente verso le pareti della camera a vuoto. Per ovviare a questo inconveniente, che impedirebbe al ciclotrone di funzionare correttamente, i poli sono sagomati in modo tale da ridurre leggermente il campo ai bordi del magnete e da incurvare le linee di forza in modo simmetrico verso i poli. Fuori dal piano mediano, il campo possiede una componente Br, ortogonale alla velocità e dipendente dal raggio; tale componente, nulla in corrispondenza del piano mediano, aumenta con la distanza da quest'ultimo. La forza di Lorentz ha perciò una componente verticale, proporzionale a Br e crescente con la distanza dal piano mediano verso il quale è diretta: in modo analogo a ciò che avviene per il pendolo, lo spostamento da una posizione di equilibrio stabile genera una forza di richiamo, il cui effetto è quello di focalizzare debolmente le traiettorie; le oscillazioni delle particelle descritte per la prima volta da Donald W. Kerst e da Robert Serber nel 1941 si chiamano oscillazioni di betatrone. La forza di Lorentz, inoltre, ha una componente orizzontale che induce un moto oscillatorio di ampiezza ϱ=r−r0 intorno all'orbita di raggio r0. In definitiva (Tav. I) se il cosiddetto indice di campo n è compreso tra 0 e 1, nell'approssimazione lineare del problema le traiettorie sono stabili e il moto risultante è oscillatorio nei due piani, con frequenze rispettive:
[3] formula .
Il moto è indipendente nelle due direzioni, ma per particolari valori di n il rapporto tra la frequenza radiale e quella verticale risulta uguale a un numero intero e si realizzano condizioni di risonanza, in cui le piccole imperfezioni magnetiche introducono nelle equazioni del moto termini di accoppiamento che provocano il trasferimento di energia da una direzione all'altra. Il fenomeno può provocare, anche nell'approssimazione lineare, una perdita di particelle e impedire il corretto funzionamento dell'acceleratore. Per ovviare a tale inconveniente, di entità tanto maggiore quanto minore è il numero che esprime il rapporto tra le due frequenze di oscillazione, occorre scegliere opportunamente il valore dell'indice di campo.
Il betatrone
In un betatrone il campo elettrico accelerante è prodotto mediante induzione magnetica, piuttosto che impiegando elettrodi o cavità a RF. Consideriamo un elettrone che percorra un'orbita circolare di raggio r immersa in un campo magnetico e indichiamo con φ=πr2〈B〉 il flusso attraverso il cerchio racchiuso nell'orbita, dove 〈B〉 è il valore medio che il campo assume all'interno dell'orbita: una variazione di φ nel tempo induce sull'elettrone una differenza di potenziale elettrico U(t)=−dφ(t)/dt su tutta la lunghezza dell'orbita, e quindi un campo elettrico tangente all'orbita stessa dato da:
[4] formula
Il valore di E è positivo o negativo a seconda del segno della derivata temporale di 〈B〉; in particolare, se 〈B〉 aumenta E sarà positivo e l'elettrone risulterà accelerato. Consideriamo ora la forma dell'orbita, sulla quale in generale potrebbe incidere l'aumento del campo magnetico e quindi la maggiore velocità dell'elettrone. La quantità di moto e l'equazione del moto dell'elettrone a un dato istante si scrivono, rispettivamente:
[5] mv = erB
[6] formula
dove B nella [5] indica il valore assunto dal campo in corrispondenza della traiettoria dell'elettrone. Una variazione di campo dB produce in un intervallo dt un incremento della quantità di moto che, se vale l'ipotesi che r non varia, è pari a d(mv)=erdB secondo la [5]; la [6] prevede invece che d(mv)=eEdt=e(r/2)d〈B〉, dove 〈B〉 è il valore medio su tutto il cerchio inscritto. Se uguagliamo le due espressioni precedenti, otteniamo una relazione che non contiene né la massa né la velocità dell'elettrone:
[7] d〈B〉 = 2dB ⇔〈B〉 = 2B.
La [7] garantisce che l'elettrone percorra una circonferenza di raggio r fino a raggiungere energie relativistiche, purché il valore medio del campo all'interno dell'orbita sia il doppio di quello assunto dal medesimo campo lungo l'orbita stessa. Tale condizione risulta soddisfatta se vi è una rapida diminuzione del campo magnetico dal centro alla periferia del polo. Un serio limite alla frequenza di funzionamento del betatrone, e quindi al numero di elettroni prodotti, è posto dal surriscaldamento del magnete, causato dalle correnti parassite indotte sul polo dalle variazioni di flusso magnetico. Tipicamente la frequenza è di 50 Hz e la fase accelerante dura circa un centesimo di secondo: l'elettrone raggiunge molto rapidamente una velocità prossima a quella della luce e percorre intorno ai 3000 km, che corrispondono a circa tre milioni di orbite se il diametro polare è di 30 cm. A ogni giro l'elettrone guadagna poco meno di 1 keV, ma emette radiazione elettromagnetica la cui intensità aumenta con la quarta potenza della quantità di moto e il cui effetto è una perdita di energia cinetica quantificabile in circa 7 eV per giro a 20 MeV.
2. Il principio di stabilità di fase e sue applicazioni
Torniamo a considerare acceleratori nei quali l'energia è fornita alle particelle da una tensione RF, siano essi lineari oppure circolari. Il principio di stabilità di fase, formulato da Vladimir Veksler in Russia e, in modo indipendente, da Edwin M. McMillan negli Stati Uniti, garantisce che in corrispondenza di un ben determinato valore di fase del campo accelerante, e per effetto del focheggiamento longitudinale, particelle leggermente sfasate possano tornare in fase rispetto alla radiofrequenza, in modo tale da addensarsi giro dopo giro in pacchetti stabili. Soffermiamoci sul caso di un acceleratore circolare: facciamo l'ipotesi che il tempo di attraversamento della regione accelerante sia trascurabile rispetto a quello che intercorre tra due attraversamenti successivi e che gli effetti acceleranti, come quello indotto dalla variazione di flusso magnetico, o deceleranti, come l'emissione di radiazione, siano trascurabili rispetto all'effetto del potenziale RF. Sia ωs la frequenza di rivoluzione di una particella sincrona, ωRF la frequenza accelerante e h il numero armonico che esprime il rapporto tra ωRF e ωs. In coordinate polari, indichiamo con θs la fase della particella sincrona che attraversa la regione accelerante e con φs la fase della tensione RF in quel momento. Se V0 è il valore massimo della tensione RF, a ogni giro la particella sincrona riceverà l'energia:
[8] ΔE = eV0senφs.
Una particella in leggero ritardo temporale δt avrà una fase θ leggermente maggiore di θs e attraverserà la tensione accelerante quando φ sarà leggermente maggiore di φs. Il principio di stabilità di fase stabilisce che la particella in ritardo riceva un impulso accelerante più elevato della particella sincrona e che, nell'approssimazione non relativistica, tenda a percorrere più rapidamente la rivoluzione successiva, riducendo così il suo ritardo rispetto alla particella sincrona. In modo analogo, una particella in anticipo su quella sincrona riceverà un impulso inferiore e tenderà a ridurre tale anticipo. Non soltanto la fase, ma anche la frequenza, l'energia e il raggio della traiettoria oscillano intorno ai corrispondenti valori di una particella sincrona: le particelle formano un pacchetto compatto entro cui oscillano longitudinalmente, con frequenza piuttosto bassa rispetto alla frequenza di rivoluzione e alle oscillazioni di betatrone. Più esattamente, la frequenza di sincrotrone è data da:
[9] formula
dove ps indica la quantità di moto della particella sincrona. Si può sfruttare la proprietà della stabilità di fase per accelerare le particelle aumentando lentamente il campo magnetico e tenendo costante la frequenza RF. Nel caso di una particella relativistica, l'orbita compie oscillazioni di betatrone nelle direzioni radiale e verticale e la posizione longitudinale compie oscillazioni di sincrotrone. Questo è il principio di funzionamento di un sincrotrone. In un sincrociclotrone si può tenere costante il campo magnetico e diminuire lentamente la frequenza della tensione RF: il raggio dell'orbita aumenta e con esso l'energia delle particelle. Infine, si può mantenere costante il raggio dell'orbita e variare lentamente sia il campo magnetico sia la frequenza RF, secondo il principio di funzionamento del protosincrotrone (Tav. II).
Il principio della focalizzazione forte dovuto a gradienti alternati
Il principio di focalizzazione forte fu formulato in modo indipendente da Nicholas C. Christophilos in Grecia nel 1950 (con un lavoro che però fu pubblicato solamente nel 1956) e da Ernest D. Courant, M. Stanley Livingston e Hartland S. Snider negli Stati Uniti nel 1952. È analogo a una ben nota proprietà dell'ottica geometrica per cui, se una coppia di lenti sottili e coassiali di lunghezza focale f1 e f2 è separata da una distanza d, la lunghezza focale complessiva f è data da:
[10] formula;
se le lenti hanno lunghezza focale uguale e opposta, in altri termini se una lente è convergente e l'altra divergente con f1=−f2, il sistema è convergente e ha lunghezza focale f=f12/d. Nel caso delle macchine acceleratrici, si dispongono lungo la loro circonferenza alcuni dipoli di uguale lunghezza, tali che uno abbia gradiente radiale con effetto focalizzante nel piano verticale e defocalizzante in quello radiale, il successivo abbia gradiente radiale di valore opposto, con effetto defocalizzante nel piano verticale e focalizzante in quello radiale, e così via; il risultato è che le traiettorie sono stabili in entrambe le direzioni trasversali. L'indice di campo n
[11] formula
avrà valori uguali e opposti in due dipoli consecutivi. Se il modulo di n è molto più grande dell'unità, le forze di richiamo diventano assai maggiori che in un acceleratore a gradiente costante e a focalizzazione debole: le ampiezze di oscillazione di betatrone risultano ridotte considerevolmente e si possono realizzare dipoli di apertura molto minore. È anche possibile riservare ai magneti funzioni separate, per cui dipoli a campo rigorosamente costante curvano le traiettorie delle particelle e quadrupoli a gradienti alternati le focalizzano lungo l'asse della camera a vuoto. In una sequenza tipica, convenzionalmente chiamata FODO (Tav. III), vi è un quadrupolo, che genera un campo che cresce linearmente con gradiente orizzontale, seguito da uno o più dipoli a campo costante, da un quadrupolo a gradiente verticale e da uno o più dipoli. Il trattamento matematico delle equazioni del moto in una struttura a gradiente alternato è alquanto complicato e daremo soltanto alcuni cenni di una formulazione semplificata nella Tav. III.
L'orbita centrale in un sincrotrone a gradiente alternato è percorsa dalle particelle che sono sincrone rispetto alla tensione RF; particelle con condizioni iniziali prossime a quelle della traiettoria sincrona percorrono orbite stabili e sono soggette alle oscillazioni di betatrone e di sincrotrone. Nei tratti occupati dai dipoli, le particelle di energia leggermente maggiore rispetto a quelle sincrone descrivono orbite più esterne, quelle che hanno energia di poco inferiore orbite più interne; piccoli scarti angolari innescano le oscillazioni di betatrone e, su tempi molto più lunghi, il moto di sincrotrone induce oscillazioni che cambiano in modo adiabatico le orbite stabili da esterne a interne. La modulazione lenta delle orbite stabili diverse dalla sincrona ha una tipica inversione di fase in corrispondenza di un valore dell'energia detto 'di transizione'. Il fenomeno dipende dalle proprietà dispersive dell'acceleratore e si può dimostrare che la variazione relativa cui è soggetta la lunghezza L dell'orbita dipende linearmente da quella della quantità di moto p. Il fattore di proporzionalità α si chiama fattore di densità della quantità di moto (momentum compaction factor):
[12] formula.
In un acceleratore a focalizzazione debole si ha α=1/(1−n) e il fattore di densità risulta maggiore di 1, mentre negli acceleratori a gradiente alternato α è sempre molto ridotto, tipicamente inferiore a 0,01. Il piccolo valore di α introduce un brusco cambiamento nella relazione tra periodi di rivoluzione e quantità di moto in corrispondenza dell'energia di transizione. La variazione relativa del periodo τ=L/v di rivoluzione vale infatti
[13] formula.
Tenuto conto che
[14] formula,
si ha:
[15] formula.
Nel caso di focheggiamento debole (n〈1 e α>1) il fattore di proporzionalità della [15] è positivo e il periodo di rivoluzione cresce in modo monotòno con la quantità di moto. Nel caso di focheggiamento forte (n≫1 e α≪1) il regime cambia: se l'energia totale E è poco più grande dell'energia di riposo E0, il fattore in parentesi quadra nella [15] è negativo e il periodo di rivoluzione decresce con la quantità di moto; se E=Et=E0/(α)1/2, il periodo di rivoluzione inizia invece a crescere. L'energia di transizione Et stabilisce il valore a partire dal quale il sincronismo tra frequenza di rivoluzione e radiofrequenza deve cambiare bruscamente fase affinché la focalizzazione longitudinale di quelle particelle che hanno quantità di moto differente dalle sincrone si possa conservare. Raggiunta l'energia Et, le fasi delle particelle sono raggruppate in pacchetti e, se non si cambiasse la fase sincrona per invertire l'andamento della tensione RF, le orbite diventerebbero instabili e il sincrotrone cesserebbe di funzionare. Per α=0,01 l'energia di transizione per protoni corrisponde a E=10E0, ossia a 8,3 GeV. Nel caso di elettroni, il problema non si pone, poiché in genere l'energia di iniezione in un sincrotrone è superiore all'energia di transizione. Esistono soluzioni tecniche molto efficienti per controllare la transizione di fase in un protosincrotrone.
Per descrivere il moto di un fascio di particelle in un acceleratore, occorre tener conto di un gran numero di fenomeni che complicano enormemente il moto di una particella singola. Lenti magnetiche sestupolari servono a compensare gli effetti che piccoli scostamenti della quantità di moto hanno sulla traiettoria e sulla frequenza di betatrone; d'altra parte, piccole imperfezioni magnetiche nei dipoli e nei quadrupoli introducono termini non lineari nelle equazioni del moto e producono risonanze e scambi di energia fra i diversi piani, rendendo caotiche le orbite e probabile la perdita di particelle nella camera a vuoto. Forze interne indotte da alte densità di carica nei fasci circolanti producono una dispersione delle frequenze di betatrone, che facilita l'innesco di meccanismi di risonanza; forze esterne, indotte da effetti di scia elettromagnetica sulla camera a vuoto, producono movimenti collettivi coerenti, amplificati da meccanismi di retroazione che rendono possibile la perdita parziale o totale del fascio. Le particelle si muovono in una camera a vuoto, in cui la pressione deve essere molto bassa per evitare collisioni con le molecole d'aria residue. Un sincrotrone a bersaglio fisso, dove il fascio circola per pochi secondi prima di essere estratto e utilizzato, richiede pressioni tra 10−7 e 10−8 atmosfere. In un collisionatore, in cui la sopravvivenza del fascio va garantita per decine di ore, i valori della pressione devono essere uno o due ordini di grandezza inferiori.
Sincrotroni a gradiente alternato per elettroni: il caso del LEP
La differenza fondamentale tra un protosincrotrone e un elettrosincrotrone risiede nell'intensità della luce di sincrotrone emessa, trascurabile nel caso dei protoni ma molto elevata per gli elettroni. Consideriamo il caso del LEP (Large electron-positron collider), in cui avveniva la collisione tra fasci di elettroni e positroni: la velocità massima di tali particelle era inferiore rispetto a quella della luce nel vuoto per meno di 20 m/h (differenza confrontabile con la velocità di una lumaca) e la loro massa aumentava di 170 mila volte rispetto a quella di riposo (più o meno il rapporto tra il peso di un elefante e quello di un topolino). La circonferenza raggiungeva una lunghezza di ben 27 km, per una ragione che ora spiegheremo. Una particella carica che descriva un'orbita circolare irraggia energia elettromagnetica, con una potenza media espressa dalla formula:
[16] formula
dove E è l'energia totale della particella e ϱ il raggio dell'orbita. La costante Cγ vale:
[17] formula.
La quantità re è il raggio classico della particella, inversamente proporzionale alla massa a riposo m0. La costante Cγ assume un valore enormemente maggiore per gli elettroni (Cγ=8,85×10−5 mGeV−3) che per i protoni (Cγ=7,79×10−18 mGeV−3). La potenza irradiata deve essere compensata dal sistema RF; come si vede dalla [16], tale potenza cresce rapidamente con l'energia delle particelle, ma d'altra parte decresce all'aumentare del raggio dell'orbita: ciò spiega le grandi dimensioni del LEP. In un anello di collisione il parametro più rilevante, insieme all'energia massima disponibile nel centro di massa, è la luminosità, ossia il prodotto dell'intensità dei due fasci, diviso per la sezione trasversale della zona di collisione e per il periodo di rivoluzione; essa, moltiplicata per la sezione d'urto di un dato processo fisico, fornisce la frequenza degli eventi prodotti durante le collisioni. In termini più precisi si ha:
[18] formula
dove N è il numero di particelle contenute in ogni pacchetto circolante, f la frequenza di rivoluzione, k il numero di pacchetti che compone un fascio e σx , σy le deviazioni standard associate alle dimensioni rispettivamente orizzontale e verticale nel punto di collisione tra i due fasci. Per massimizzare la luminosità occorre massimizzare la densità e il numero dei pacchetti nel punto di collisione, per esempio mediante quadrupoli disposti in modo da agire come un microscopio che focalizzi i due fasci in entrambe le direzioni trasversali. Nel caso di elettroni e positroni, l'emissione di radiazione di sincrotrone riveste un ruolo fondamentale. Lo spettro dei fotoni emessi è contraddistinto dalla cosiddetta energia critica, definita come quel valore per il quale vi sono tanti fotoni che hanno energia maggiore quanti sono quelli con energia minore; tale energia critica, indicata con ε vale:
[19] formula
dove h è la costante di Planck, γ=(1−β2)−1/2 il fattore relativistico e ϱ il raggio dell'orbita. I fasci di 55 GeV utilizzati alla fine degli anni Ottanta del XX sec. nel LEP, per esempio, emettevano uno spettro di fotoni la cui energia critica era di 119 keV. Utilizzando la [16] possiamo calcolare l'energia emessa da un elettrone durante una rivoluzione nel LEP:
[20] formula.
Elettroni di 55 GeV perdono 260 MeV per giro, a fronte di una tensione RF accelerante il cui valore di picco è 400 MV. L'energia emessa sotto forma di radiazione di sincrotrone induce uno smorzamento delle oscillazioni di betatrone orizzontali e verticali e delle oscillazioni di sincrotrone (oscillazioni di energia). Nel LEP, a 55 GeV il tempo di smorzamento delle oscillazioni verticali era τy=37,8 ms. La deviazione standard σE della distribuzione di energia del fascio è un parametro importante, determinato da due opposti fenomeni: le oscillazioni di betatrone e di sincrotrone tendono a smorzarsi a causa dell'energia media emessa, ma d'altra parte tendono a essere eccitate per via del fatto che l'emissione coinvolge fotoni ed è quindi di natura discreta. Le oscillazioni di sincrotrone obbediscono all'equazione del moto di un oscillatore armonico, smorzato da una forza di natura stocastica. Fra gli effetti collettivi che hanno luogo in un anello di collisione ricordiamo inoltre l'interazione elettromagnetica tra i fasci collidenti: la corrente circolante in ciascun fascio esercita sulle particelle dell'altro una forza di Lorentz di considerevole intensità, che dipende in modo non lineare dallo spostamento della particella rispetto all'altro fascio.
Breve storia degli anelli di collisione
Un acceleratore dedicato allo studio dei fenomeni subnucleari dovrebbe garantire sia alte energie sia un elevato numero di eventi, ma negli anelli di collisione la probabilità d'interazione è in genere piuttosto bassa. Nella seconda metà degli anni Cinquanta, si cominciò a studiare la possibilità di costruire anelli in grado di accumulare per tempi lunghi notevoli quantità di carica. Nel 1957 un gruppo di fisici della Midwestern University Research Association (MURA) negli Stati Uniti propose una nuova tecnica di accumulazione di particelle (particle stacking), che consisteva nell'iniettare un fascio di protoni su un'orbita circolare vicina alla regione interna della camera a vuoto; le particelle erano poi accelerate mediante un'appropriata tensione RF, mantenendo costante il campo magnetico deflettente: l'orbita si spostava verso la parete esterna della ciambella a vuoto. Il ciclo di iniezione sull'orbita interna e di accelerazione fino a quella esterna era ripetuto più volte e portava a un'accumulazione notevole di carica, ottenuta la quale l'intero fascio era rallentato e disposto sull'orbita chiusa al centro della camera a vuoto. La chiave del successo fu lo sviluppo di un sofisticato sistema per controllare la frequenza e l'ampiezza della tensione RF durante la fase di accumulazione delle cariche. Sul finire degli anni Sessanta questo metodo, opportunamente perfezionato, fu applicato all'anello di accumulazione ISR (Intersecting storage ring) del CERN (Conseil Européen pour la Recherche Nucléaire) e permise di raggiungere correnti continue di protoni di oltre 30 A, per tempi di accumulazione di una cinquantina di ore, con energie di collisione di 62 GeV nel centro di massa e con luminosità di 1,4∙1032 cm−2s−1. L'ISR permise di studiare per la prima volta, con costi relativamente contenuti, le collisioni fra protoni in condizioni di altissima energia e luminosità.
Il primo anello di collisione fra elettroni e positroni fu proposto da Bruno Touschek nel 1960 per studiare le interazioni nella regione temporale dello spazio delle fasi e chiarire la dinamica dei processi nei quali l'elettrone e il positrone si disintegrano in fotoni virtuali, per poi generare nuove particelle. L'acceleratore suggerito da Touschek, chiamato ADA (Anello di accumulazione), aveva un solo anello nel quale fasci di elettroni e positroni di 250 MeV potevano ruotare simultaneamente in direzioni opposte, incontrandosi in più punti lungo la circonferenza. Nello stesso periodo, a Stanford negli Stati Uniti, Gerard O'Neill proponeva di costruire due anelli tangenti nei quali accumulare elettroni di 300 MeV. Le collisioni nel punto di tangenza permettevano di investigare la regione spaziale dello spazio delle fasi, complementare a quella temporale. Gli anelli di collisione elettrone-positrone ebbero un ruolo fondamentale nello studio della fisica delle particelle, a causa dell'estrema semplicità dello stato iniziale e degli scarsi processi spuri. Qualche anno dopo la costruzione di ADA, a Novosibirsk in Russia furono costruiti in rapida sequenza due acceleratori elettrone-positrone, VEPP-I e VEPP-II, quest'ultimo con un'energia nel centro di massa di 769 MeV: fu il primo acceleratore con il quale furono rilevate reazioni di annichilazione.
Negli anni successivi in diverse parti del mondo fu costruita una serie considerevole di anelli elettrone-positrone di energie crescenti, che permisero un sostanziale progresso nella comprensione della fisica delle particelle: nel 1967 entrò in funzione ACO (Anneau de collisions d'Orsay) in Francia, con energia di 1,1 GeV; nel 1970 Adone a Frascati, con collisioni di 3 GeV; nel 1973 si ottennero a Cambridge (USA) collisioni di 5 GeV nel centro di massa; l'anno successivo fu la volta di SPEAR (Stanford positron electron accelerating ring) in California (8,4 GeV) e di DORIS (Doppel Ring Speicher) ad Amburgo in Germania (10 GeV); nel 1978 PETRA (Positron electron tandem ring accelerator) ad Amburgo (38 GeV); nel 1979 CESR (Cornell electron storage ring) negli Stati Uniti (16 GeV), seguito da TRISTAN in Giappone e SLC (Stanford linear collider). Infine, nel luglio del 1989, al CERN di Ginevra entrò in funzione il LEP che, grazie all'uso massiccio di cavità superconduttrici di nuova generazione, raggiunse un'energia di poco superiore ai 200 GeV. Lo sviluppo di cavità superconduttrici che permettono elevate tensioni RF con consumi elettrici ridotti è la chiave del successo per ottenere energie così elevate in un sincrotrone. Probabilmente il LEP è stato l'ultimo acceleratore della sua generazione, poiché sembra ormai escluso che si possa aumentare ulteriormente l'energia dei fasci e contrastare l'effetto della radiazione di sincrotrone con cavità ancora più potenti: la via aperta da ADA sembra irrimediabilmente chiudersi e sono già in progetto acceleratori lineari di alta intensità per fasci collidenti elettrone-elettrone o elettrone-positrone ben oltre la soglia del centinaio di GeV.
Il primo anello di collisione protone-protone e protone-antiprotone fu il già menzionato ISR, operante al CERN dal 1971 al 1984, che chiarì molte delle caratteristiche che concorrevano a un funzionamento ottimale degli anelli di collisione a protoni e stimolò nuove strategie di progettazione per esperimenti e apparati sperimentali. La sua costruzione fu intrapresa tra grandi perplessità: la prima riguardava la luminosità, assai piccola se confrontata con quella di acceleratori convenzionali a bersaglio denso fisso; la seconda la stabilità dei fasci per periodi di accumulazione di parecchie ore. Con l'ISR si dimostrò che esistevano soluzioni per entrambi i problemi. In seguito furono progettati altri tre anelli protone-protone: l'UNK in Russia, l'SSC negli Stati Uniti e il Large hadron collider (LHC) del CERN, ma l'esecuzione dei primi due fu interrotta per ragioni economiche all'inizio degli anni Novanta.
La produzione di densi fasci di antiprotoni, richiedendo una riduzione della considerevole dispersione in angolo e in energia, si rivelò particolarmente complessa e fu resa possibile dal raffreddamento mediante elettroni, ideato da Gersh I. Budker nel 1967, e dal raffreddamento stocastico, dovuto a Simon van der Meer nel 1968. Il raffreddamento stocastico impiega un sistema di alta frequenza che permette di misurare e correggere le oscillazioni di traiettoria e di fase RF. Il successo del metodo dipende da due aspetti: il sistema deve funzionare su una larga banda di frequenze e i dispositivi devono avere un bassissimo rumore elettronico. I primi esperimenti di raffreddamento stocastico ebbero luogo nel 1972 nell'ISR, e in un anello detto ICE (Initial cooling experiment), sempre al CERN, sul finire degli anni Settanta. Nel 1976 Carlo Rubbia propose di trasformare il protosincrotrone SPS (Super proton synchroton) del CERN in un anello di collisione protone-antiprotone. Fu costruito un efficientissimo anello di accumulazione per antiprotoni mediante il quale alimentare l'SPS e quest'ultimo divenne un anello di collisione in cui protoni e antiprotoni, accelerati fino a 270 GeV (successivamente a 315 GeV), collidevano in più punti. Il successo fu straordinario, sia perché favorì la comprensione profonda della fisica degli anelli di collisione, sia perché furono osservati per la prima volta direttamente i bosoni vettoriali W e Z, protagonisti, insieme al fotone, dell'unificazione delle interazioni elettromagnetiche e deboli: la teoria elettro-debole ipotizzata alcuni decenni prima trovava una clamorosa conferma, che sarebbe stata resa ancora più solida e chiara alcuni anni dopo dai risultati del LEP.
Una conversione analoga a quella subita dall'SPS spettò successivamente al protosincrotrone del Fermilab (USA), trasformato in un anello di collisione, detto TEVATRON, in cui circolavano fasci di protoni e antiprotoni di 800 GeV. Qui fu osservato il quark top, che completa il panorama dei costituenti nucleari. Vogliamo ancora menzionare due anelli di collisione unici nel loro genere, HERA (Hadron electron ring accelerator) ad Amburgo e RHIC (Relativistic heavy ion collider) negli Stati Uniti. Entrato in funzione nel 1991, HERA è il primo anello di collisione di elettroni e protoni: comprende l'anello di elettroni di PETRA, leggermente modificato per incrementare l'intensità e funzionare fino a 30 GeV, e un anello che permette di accelerare protoni fino a 820 GeV, costruito con magneti superconduttori interamente realizzati dall'industria europea. RHIC è invece un anello di collisioni per ioni di qualunque specie, costituito da due anelli intrecciati capaci di accelerare nuclei completamente ionizzati fino a 200 GeV per nucleone.
Anelli di collisione per protoni: il caso LHC
L'anello di collisione per adroni Large hadron collider (LHC) è in fase di costruzione al CERN di Ginevra, insieme a quattro apparati sperimentali (CMS, ATLAS, ALICE e LHCb) destinati allo studio delle reazioni che si produrranno nei quattro punti di incrocio; dovrebbe essere completato nel 2007. L'acceleratore è costituito da due anelli intersecantisi ed è installato all'interno della galleria circolare di 27 km che ha ospitato il LEP, prima che questo smettesse di funzionare, nel novembre del 2000. Il LHC ha un'energia di collisione di 14 TeV e una luminosità di 1034cm−2s−1 (venti volte quella dell'ISR). I dipoli e i quadrupoli sono magneti superconduttori raffreddati da elio superfluido a 1,9 K, con bobine di niobio e titanio a due strati; al momento delle collisioni il campo dipolare supera gli 8 Tesla. Per ridurre i costi, l'apertura delle bobine è di soli 56 mm di diametro e la struttura meccanica contiene entrambi i canali magnetici che costituiscono i due anelli di LHC. In condizioni operative, la forza elettromagnetica esercitata dalla bobina sulla struttura di contenimento di un dipolo lungo 15 m è di circa 100.000 t: i conduttori tendono a deformarsi e nel campo magnetico appaiono distorsioni non lineari, il cui valore relativo è di alcune parti su diecimila; anche la forza elettromagnetica tra i fasci e le correnti nel superconduttore producono forze non lineari, che rendono caotiche e instabili le orbite dei protoni. Per valutare questi effetti sono stati sviluppati sofisticati strumenti di analisi e di calcolo e, per mitigarne le conseguenze, sono stati posti in opera accurati sistemi di controllo per la qualità dei componenti critici, quali cavi superconduttori, bobine e collari di contenimento; per bilanciare gli effetti negativi delle componenti non lineari del campo sono stati installati correttori magnetici.
In un anello di collisione, la sezione d'urto di un evento è correlata all'inverso del quadrato della massa prodotta. Quanto maggiore è l'energia di collisione, tanto più elevata deve essere la luminosità. A questo riguardo, il principale limite fisico nasce proprio dall'interazione coulombiana tra fasci di protoni collidenti, le cui traiettorie hanno comportamento stocastico e risultano destabilizzate allorché la densità dei pacchetti supera un dato valore. L'interazione elettromagnetica tra il fascio di particelle e le pareti metalliche del contenitore toroidale pone un'ulteriore limitazione: allorché l'intensità di carica circolante supera un certo valore, la carica immagine nelle pareti induce un effetto destabilizzante. Limiti di natura tecnologica sorgono poi nel definire le caratteristiche di alcuni sistemi di importanza strategica: quello criogenico, per esempio, oltre a raffreddare i magneti, deve assorbire la potenza irradiata sotto forma di radiazione di sincrotrone e quella depositata quando avviene la perdita del fascio. Il sistema destinato ad assorbire i protoni ancora circolanti alla fine di una sessione sperimentale deve essere anche in grado di affrontare situazioni di emergenza, nel caso l'enorme quantità di energia immagazzinata nel fascio dovesse essere liberata in tempi brevissimi. Il sistema di collimazione deve avere un'elevatissima efficienza, per evitare perdite parassitiche nei magneti freddi, e d'altra parte in caso di emergenza deve poter assorbire senza danneggiarsi l'impatto di una considerevole parte del fascio. Infine, la camera a vuoto, di esigue dimensioni, è priva di pompe e sfrutta l'effetto di pompaggio criogenico diffuso tra superfici a temperature diverse.
Gli acceleratori hanno svolto un ruolo fondamentale nello sviluppo della fisica delle alte energie, poiché hanno messo a disposizione condizioni ideali e ben riproducibili per indagare le leggi del mondo microscopico. Il loro impiego si è esteso ad altre branche della scienza, tra cui la medicina e la biologia, e ad applicazioni industriali e tecnologiche di vario tipo. I primi acceleratori hanno permesso di studiare i costituenti fondamentali della materia: elettroni, protoni, neutroni, neutrini e le loro antiparticelle. Via via che l'energia è aumentata, si sono potute mettere in evidenza entità più nascoste, come i quark e una miriade di altre particelle con vita media brevissima e massa talora superiore a quella dei protoni stessi. Gli anelli di collisione hanno permesso recentemente di esplorare energie di oltre 100 GeV, talmente elevate da consentire la produzione di bosoni pesanti, come il W e lo Z, e rivelare l'esistenza di simmetrie interpretabili nell'ambito di teorie sempre più complete. Nel futuro immediato si spera che l'anello di collisione LHC, in costruzione al CERN, possa mettere in evidenza simmetrie ancora più nascoste, capaci di contribuire all'unificazione della nostra visione del mondo microscopico.
Bibliografia
Amaldi 1981: Amaldi, Edoardo, The Bruno Touschek legacy, Genève, CERN 81-19, 1981.
Barber 1966: Barber, Walter C. e altri, Test of quantum electrodynamics by electron-electron scattering, "Physical review letters", 16, 1966, pp. 1127-1130.
Bernardini 1962: Bernardini, Carlo e altri, Progress report on ADA (Frascati storage ring), "Nuovo cimento", 23, 1962, pp. 202-207.
Bryant, Johnsen 1993: Bryant, Philip J. - Johnsen, Kiell, The principle of circular accelerators and storage rings, Cambridge, Cambridge University Press, 1993.
Budker 1967: Budker, Gersh I., Status report of works on storage rings at Novosibirsk, in: Proceedings of the International symposium on electron-positron storage rings (Saclay, 1966), Paris, P.U.F., 1967, pp. 1-3.
Budker, Skrinsky 1978: Budker, Gersh I. - Skrinsky, Alexander N., Electron cooling and new possibilities in elementary particle physics, "Soviet physics-Uspekhi", 21, 1978, pp. 277-296.
Christofilos 1956: Christofilos, Nicholas, Focusing system for ions and electrons, US Patent No. 2.736.799 filed March 10, 1950 issued February 28, 1956.
Cline 1991: Cline, David B. - Rubbia, Carlo - van der Meer, Simon, Alla ricerca dei bosoni vettoriali intermedi, in: Campi, forze e particelle, a cura di Luciano Maiani, Milano, Le scienze, 1991, pp. 12-24.
Cockcroft, Walton 1932: Cockcroft, John D. - Walton, Ernest T.S., Experiments with high velocity positive ions. I. Further developments in the method of obtaining high velo_city positive ions, "Proceedings of the Royal Society of London. Series A", 136, 1932, pp. 619-630.
Courant 1952: Courant, Ernest D. - Livingston, M. Stanley - Snyder, Hartland S., The strong-focusing synchrotron. A new high energy accelerator, "Physical review", 88, 1952, pp. 1190-1196.
Haissinski 1998: Haissinski, Jacques, From ADA to ACO, in: Bruno Touschek and the birth of e+e- physics, a cura di Gino Isidori, Frascati, Laboratori Nazionali di Frascati dell'INFN, 1998, pp. 17-31.
Kerst 1941: Kerst, Donald W., The acceleration of electrons by magnetic induction, "Physical review", 60, 1941, pp. 47-53.
Kerst, Serber 1941: Kerst, Donald W. - Serber, Robert, Electronic orbits in the induction accelerator, "Physical review", 60, 1941, pp. 53-58.
Kohaupt, Voss 1983: Kohaupt, Rolf-Dieter - Voss, Gustav-Adolf, Progress and problems in performance of e+e- storage rings, "Annual review of nuclear and particle science", 33, 1983, pp. 67-104.
Lawrence 1952: Lawrence, Ernest O., The evolution of the cyclotron, in: Les Prix Nobel en 1951, Stockholm, Imprimerie Royale, Norsted & Soner, 1952, pp. 127-140.
Lederman 1991: Lederman, Leon M., Il tevatron, in: Campi, forze e particelle, a cura di Luciano Maiani, Milano, Le scienze, 1991, pp. 104-112.
Livingston, Blewett 1962: Livingston, M. Stanley - Blewett, John P., Particle accelerator, New York, McGraw-Hill, 1962.
McMillan 1945: McMillan, Edwin M., The synchrotron, a proposed high energy particle accelerator, "Physical review", 68, 1945, pp. 143-144.
Myers, Picasso 1990: Myers, Stephen - Picasso, Emilio, The design, costruction and commissioning of the CERN electron-positron collider, "Contemporary physics", 31, 1990, pp. 387-403.
Nilsen 1956: Nilsen, Nils V., Attainment of very high energy by means of intersecting beam particles, "Physical review", 102, 1956, pp. 590-591.
O'Neill 1956: O'Neill, Gerard K., Storage-ring synchrotron: device for high-energy physics research, "Physical review", 102, 1956, pp. 1418-1419.
Picasso, Ruggiero 1988: Picasso, Emilio - Ruggiero, Francesco, Alcune considerazioni relative alla costruzione di LEP, "Il nuovo saggiatore", 4, 1988, pp. 16-51.
Picasso, Ruggiero 2004: Picasso, Emilio - Ruggiero, Francesco, Gli acceleratori di particelle, in: Storia della scienza, Roma, Istituto della Enciclopedia Italiana, 2004, IX, pp. 145-159.
Rubbia 1985: Rubbia, Carlo, Experimental observation of the intermediate vector boson W+, W-, Z0, "Reviews of modern physics", 57, 1985, pp. 699-722.
Salvini 1980: Salvini, Giorgio, Particelle elementari: acceleratori, in: Enciclopedia del Novecento, Roma, Istituto della Enciclopedia Italiana, 1980, V, pp. 215-238.
Schopper 1998: Advances of accelerator physics and technologies, edited by Herwing Schopper, Singapore-London, World Scientific, 1998 (1. ed.: 1993).
Sloan, Lawrence 1931: Sloan, David H. - Lawrence, Ernest O., The production of heavy high speed ions without the use of high voltage, "Physical review", 38, 1931, pp. 2021-2031.
Van der Meer 1972: van der Meer, Simon, Stochastic damping of betatron oscillations in the ISR, CERN/ISR-PO, 72-31, august 1972, Geneva, CERN, 1972.
Van der Meer 1985: van der Meer, Simon, Stochastic cooling and the accumulation of antiprotons, "Reviews of modern physics", 57, 1985, pp. 689-697.
Veksler 1945: Veksler, Vladimir, A new method of acceleration of relativistic particles, "Journal of physics, USSR", 9, 1945, pp 153-158.
Wideröe 1928: Wideröe, Rolf, A new principle for the generation of high voltage, "Archiv für Elektrotechnik", 21, 1928, pp. 387-406.